Traccia

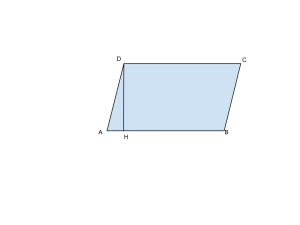
Determinare l’area di un parallelogramma di cui si conoscono due lati consecutivi (cm 8 e cm 6) e l’ampiezza dell’angolo compreso ().

Svolgeremo questo esercizio con i radianti. Se ci fossero problemi con il loro utilizzo, basta eseguire la seguente sostituzione:

.

 

Svolgimento

 

 

Dai dati avremo che:

Poi, sappiamo che in un quadrilatero qualsiasi, la somma degli angoli interni è , ed avendo il parallelogramma angoli uguali a 2 a 2, avremo che:

e

.

 

Da qui possiamo ricavare subito l’altezza DH, sapendo che:

.

 

Da qui possiamo calcolare l’area del parallelogramma:

 

 

 

 

Altri esercizi simili

• Esercizio 1 Problema di geometria piana risolubili con l’uso della trigonometria.
• Esercizio 2 Problema di geometria piana risolubili con l’uso della trigonometria
• Esercizio 3 Problema di geometria piana risolubili con l’uso della trigonometria
• Esercizio 4 Problema di geometria piana risolubili con l’uso della trigonometria
• Esercizio 5 Problema di geometria piana risolubili con l’uso della trigonometria

(Questa pagina è stata visualizzata da 192 persone)