Esercizio 6 Problemi di geometria

Traccia

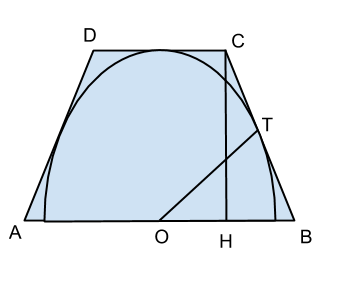
Un trapezio isoscele è circoscritto a una semicirconferenza di diametro 30 cm. Dopo aver dimostrato che il lato obliquo è metà della base maggiore, determinare il perimetro del trapezio sapendo che il diametro è il triplo della base minore.

Svolgimento

Tracciamo l’altezza CH ed il raggio OT, essendo T il punto di tangenza di un lato obliquo.

L’angolo $\widehat{OTB}$ risulta retto per il teorema della retta tangente.

I triangoli rettangoli CHB e OTB sono congruenti per il criterio dei triangoli rettangoli (CH = OT perché raggi; l’angolo in B in comune).

Di conseguenza

$BC = OB = \frac 12 AB$ cvd.

Dai dati avremo che:

$CD=10 \mbox { cm}$ .

Poniamo

$BC=x$

$AB=2x$

e così avremo:

$BH=\frac 12 (2x-10)=x-5$

Sfruttiamo il triangolo rettangolo CHB per ricavare la x, sapendo che l’altezza equivale al raggio:

$CB^2=CH^2+HB^2$

$x^2=15^2+(x-5)^2$

$x^2=225+x^2-10x+25$

$10x=250$

$x=25$

Quindi otteniamo:

$BC= 25 \mbox { cm}$

$AD = 25 \mbox { cm}$

$AB= 50 \mbox { cm}$

Il perimetro sarà:

$2p_{ABCD}=(50+25+10+25) \mbox { cm}=110\mbox { cm}$

Altri esercizi simili:

(Questa pagina è stata visualizzata da 114 persone)

Matebook

La matematica spiegata passo passo

Esercizio 6 Problemi di geometria

Lascia un commento Annulla risposta