Esercizio 9 Problemi di geometria

-2

Traccia

Nel triangolo isoscele ABC, la base BC è congruente all’altezza AH a essa relativa: si sa, inoltre che la differenza fra i \frac34 di BC e i \frac 23 di AH è 4 cm. Determinare il diametro della circonferenza circoscritta al triangolo. 60

Svolgimento

triangolo isoscele inscritto

Dai dati avremo:

BC=AH

\frac 34 BC - \frac 23 AH=4

Poniamo BC=x

\frac 34x -\frac 23 x =4

9x-8x=48

x=48

Quindi avremo che:

BC=AH=48 \mbox { cm}

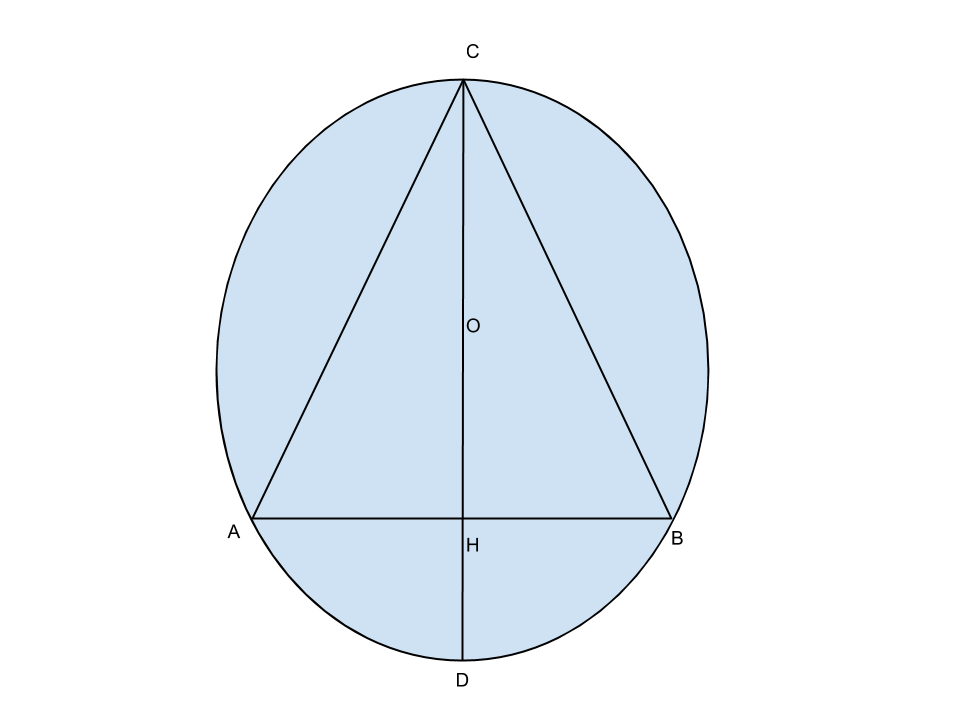
Da qui calcoliamo il diametro con Euclide, notando che, prolungando l’altezza affinchè incontri la circonferenza nel punto D, avremo che ABD  è un triangolo rettangolo:

DH=\frac {BH^2}{AH}=\frac {24^2}{48}\mbox { cm}=\frac {576}{48}\mbox { cm}=12\mbox { cm}.

Il diametro quindi sarà:

AD=AH+HD=(48+12) \mbox { cm}=60 \mbox { cm}.

 

 

 

Altri esercizi simili:

(Questa pagina è stata visualizzata da 110 persone)

Lascia un commento