Traccia
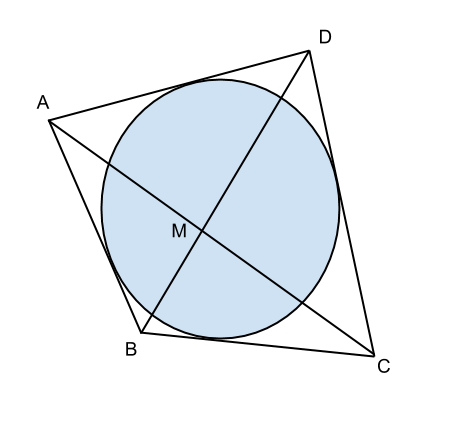
Il quadrilatero ![]() ha la diagonale maggiore
ha la diagonale maggiore ![]() perpendicolarae alla diagonale minore
perpendicolarae alla diagonale minore ![]() nel suo punto medio
nel suo punto medio ![]() . Determinare le lunghezze delle diagonali sapendo che la loro somma è 49 m e che la differenza tra i
. Determinare le lunghezze delle diagonali sapendo che la loro somma è 49 m e che la differenza tra i ![]() della maggiore e i
della maggiore e i ![]() della minore è 26 m. Sapendo inoltre che
della minore è 26 m. Sapendo inoltre che ![]() , determinare le lunghezze dei lati del quadrilatero e verificare che gli angoli in
, determinare le lunghezze dei lati del quadrilatero e verificare che gli angoli in ![]() e in
e in ![]() sono retti. Dopo aver dimostrato che il quadrilatero è circoscrivibile a una circonferenza, determinare il raggio della circonferenza inscritta.
sono retti. Dopo aver dimostrato che il quadrilatero è circoscrivibile a una circonferenza, determinare il raggio della circonferenza inscritta.
Svolgimento
Dai dati avremo che:
![]()
![]()
Ponendo ![]() otteniamo:
otteniamo:
![]()
e sostituendo avremo:
![]()
![]()
![]()
![]()
![]()
Quindi avremo:
![]()
e
![]() .
.
Sappiamo ancora dai dati che:
![]()
![]()
e notando che:
![]()
avremo:
![]()
![]()
![]()
![]() .
.
Per verificare che gli angoli in B e in D siano retti, basterà verificare il secondo teorema di Euclide sul triangolo ABC, che quindi ipotizziamo retto in B. Se fosse vero, deve verificarsi che:
![]()
![]()
![]() CVD.
CVD.
Calcoliamo le lunghezze dei lati con Pitagora:
![]() .
.
![]() .
.
Affinchè sia circoscrivibile deve verificarsi che la somma dei lati opposti sia uguale, ma questo è verificato perchè i lati sono uguali a due a due consecutivamente:
![]()
![]() CVD.
CVD.
Il raggio della circonferenza inscritta sarà dato da:
![]() , dove
, dove
![]() .
.
![]() .
.
Quindi:
![]() .
.
Altri esercizi simili:
- Esercizio 1 Problema di geometria
- Esercizio 2 Problema di geometria
- Esercizio 3 Problema di geometria
- Esercizio 4 Problema di geometria
- Esercizio 5 Problema di geometria
- Esercizio 6 Problemi di geometria
- Esercizio 7 Problemi di geometria
- Esercizio 8 Problemi di geometria
- Esercizio 9 Problemi di geometria
- Esercizio 10 Problemi di geometria
- Esercizio 11 Problemi di geometria
- Esercizio 12 Problemi di geometria
- Esercizio 13 Problemi di geometria
- Esercizio 14 Problemi di geometria
- Esercizio 15 Problemi di geometria
- Esercizio 16 Problemi di geometria
- Esercizio 17 Problemi di geometria
- Esercizio 18 Problemi di geometria
- Esercizio 19 Problemi di geometria
- Esercizio 20 Problemi di geometria
- Esercizio 21 Problemi di geometria
- Esercizio 22 Problemi di geometria
- Esercizio 23 Problemi di geometria
- Esercizio 24 Problemi di geometria
- Esercizio 25 Problemi di geometria
- Esercizio 26 Problemi di geometria
(Questa pagina è stata visualizzata da 86 persone)