Esercizio 16 Problemi di geometria

0

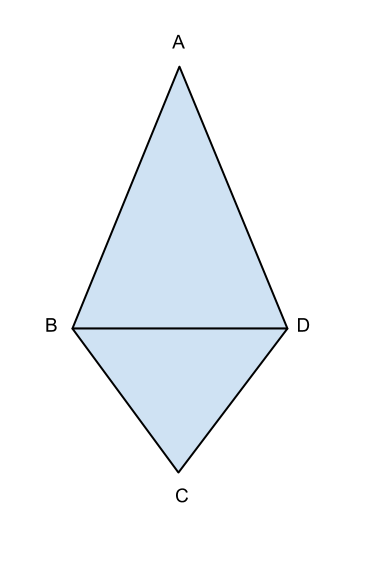
Traccia

I triangoli isosceli ABD e CBD hanno in comune la base BD e i vertici A e C giacciono da parte opposta rispetto alla base BD. Le misure dei perimetri dei triangoli sono rispettivamente 64a e 54a. Determinare le misure dei lati dei triangoli sapendo che:

    \[\frac 45 BC - \frac 14 AB = 7a\]

Verificare che gli angoli in B e in D del quadrilatero ABCD sono retti e determinare la misura del raggio della circonferenza circoscritta al quadrilatero.

Svolgimento

triangoli isosceli

Dai dati abbiamo che:

2AB+BD=64a

2BC+BD=54a

da cui:

AB-BC=5a.

Sappiamo inoltre che

\frac 45 BC - \frac 14 AB=7a.

Mettendo a sistema otteniamo, ponendo AB=x e BC=y

\begin{cases} x-y=5a \\ \frac 45 y - \frac 14x=7a \end{cases}

\begin{cases} x=5a+y \\ \frac 45 y - \frac 54a - \frac 14y=7a \end{cases}

\begin{cases} x=5a+y \\ 16 y - 25a - 5y=140a \end{cases}

\begin{cases} x=5a+y \\ 11 y =165a \end{cases}

\begin{cases} x=20a \\ y =15a \end{cases}.

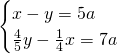
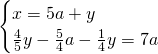
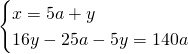
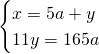
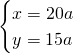Trovati i lati, ci serve verificare che B e D siano retti, sapendo che, dai risultati precedenti, BD=24a.

AM=\sqrt {AB^2-BM^2}=\sqrt {400-144}a=16a

CM=\sqrt {CB^2-BM^2}=\sqrt {225-144}a=9a

se B fosse retto si deve verificare che:

AC=AM+MC=25a=\sqrt {AB^2+BC^2}=\sqrt{400+225}a=\sqrt{625}a=25a CVD.

Ora, visto che ABC e CDA sono rettangoli, evidentemente ognuno di questi triangoli è inscritto in una semicirconferenza e di conseguenza, AC risulterà essere il diametro, quindi:

r=\frac 12 AC=12,5 a.
 

Altri esercizi simili:

(Questa pagina è stata visualizzata da 103 persone)

Lascia un commento