Esercizio 20 Problemi di geometria

-1

Traccia

Nel triangolo ABC i lati AB e AC superano rispettivamente di 28 cm e 8 cm le loro proiezioni BH e CH sul lato BC. Si conosce il perimetro del triangolo, 504 cm, e si chiede di determinare i lati del triangolo, l’altezza AH, l’area del triangolo e il raggio del cerchio inscritto nel triangolo.

Svolgimento

triangolo e circonferenza

Ponendo BH=x e CH=y, otteniamo dai dati:

BC=x+y

AB=x+28

AC=y+8

Sappiamo che 2p=504 \mbox { cm}, e quindi:

x+28+y+8+x+y=504

2x+2y+36=504

x+y=234

Per avere l’altra equazione ci basterà porre, col teorema di Pitagora le uguaglianze:

AH^2=AB^2-BH^2 e

AH^2=AC^2-CH^2

Il sistema sarà quindi:

\begin {cases} x+y=234 \\ (x+28)^2-x^2=(y+8)^2-y^2\end{cases}

\begin {cases} x+y=234 \\ x^2+56x+784-x^2=y^2+16y+64-y^2\end{cases}

\begin {cases} x+y=234 \\ 56x-16y=-720\end{cases}

\begin {cases} y=234-x \\ 7x-2y=-90\end{cases}

\begin {cases} y=234-x \\ 7x-2(234-x)=-90\end{cases}

\begin {cases} y=234-x \\ 7x-468+2x=-90\end{cases}

\begin {cases} y=234-x \\ 9x=378\end{cases}

\begin {cases} y=192 \\ x=42\end{cases}

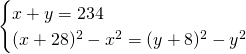
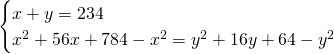
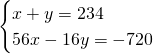
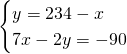
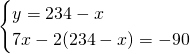
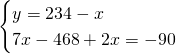
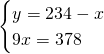
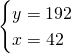
Ora possiamo ricavare praticamente tutto:

BC=234 \mbox { cm}

AB=70\mbox { cm}

AC=200\mbox { cm}

AH=\sqrt{4900-1764}\mbox { cm}=\sqrt {3136}\mbox { cm}=56 \mbox { cm}

A_{ABC}=\frac {AH \cdot BC}{2}=\frac {56 \cdot 234}{2}\mbox { cm}^2=6552 \mbox { cm}^2

Il raggio del cerchio inscritto sarà:

r= \frac {A}{p}=\frac {6552}{\frac 12 504}\mbox { cm}=26\mbox { cm}

 
 

Altri esercizi simili:

 

(Questa pagina è stata visualizzata da 97 persone)

Lascia un commento