Esercizio 23 Problemi di geometria

-1

Traccia

in un triangolo rettangolo la somma dei \frac 78 del cateto maggiore e dei \frac 23 del cateto minore è 44 a; sottraendo ai \frac 54 del cateto minore i \frac 38 del cateto maggiore si ottiene 18a . Determinare le lunghezze dei lati del triangolo e del raggio della circonferenza inscrittta dopo aver dimostrato che il diametro della circonferenza inscritta è congruente alla differenza tra la somma dei cateti e l’ipotenusa.

Svolgimento

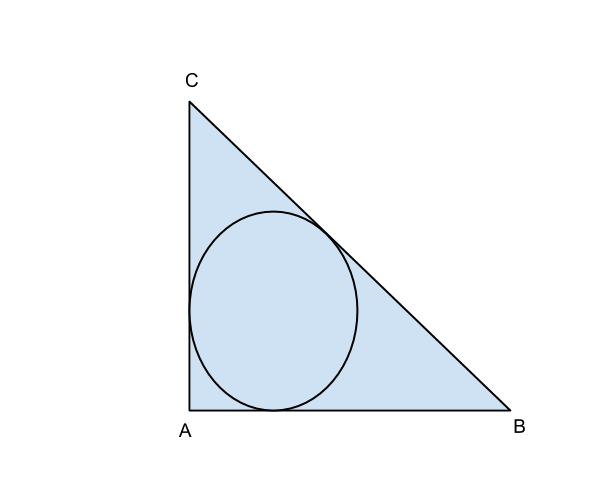
triangolo rettangolo circonferenza inscritta

Sia ABC rettangolo in A, e poniamo:

AB=x \, \, \mbox { e } \, \, AC=y,

così da avere il sistema:

\begin{cases} \frac 78x + \frac 23 y=44a\\ \frac 54y-\frac 38x=18a \end{cases}

\begin{cases} 21x + 16 y=1056a\\ 10y-3x= 144a \end{cases}

Usiamo il metodo di riduzione moltiplicando la seconda equazione per 7 e sommando le due:

\begin{cases} 21x + 16 y+70y-21x=1056a+1008a\\ 10y-3x= 144a \end{cases}

\begin{cases} 86 y=2064a\\ x=\frac 13(10y- 144a) \end{cases}

\begin{cases} y=24a\\ x=\frac 13(240a- 144a) \end{cases}

\begin{cases} y=24a\\ x=32a \end{cases}

Ricaviamo l’ipotenusa applicando pitagora:

BC=\sqrt{AC^2+AB^2}=\sqrt{(32a)^2+(24a)^2}=\sqrt{1600a^2} = 40a

Per dimostrare la richiesta della traccia, poniamo:

OM \perp AC

ON \perp AB

OP \perp BC.

Si nota che il quadrilatero OMAN risulta essere proprio un quadrato con il lato uguale al raggio.

Sappiamo per costruzione di triangolo circoscritto che:

CM = CP

AM = AN = r

BN = BP.

Si avrà quindi:

AC = CM + r

AB = BN + r

Sommandoli otteniamo:

AB + AC = CM + r + BN + r = CP + BP + 2r=BC+2r

Riscrivendo meglio avremo proprio che, considerando la prima e l’ultima uguaglianza:

AB+AC-BC=2r.

Calcoliamo ora il raggio:

r = \frac 12 (24a+32a-40a)=\frac 12 (16a)=8a.

 

 

 

Altri esercizi simili:

(Questa pagina è stata visualizzata da 83 persone)

Lascia un commento