Esercizio 25 Problemi di geometria

Traccia

Nel triangolo $ABC$ , rettangolo in $A$ , il cateto minore $AB$ è lungo $7a$ e l’ipotenusa supera di $a$ l’altro cateto. Determinare sull’ipotenusa $BC$ un punto $P$ in modo che sia

$\frac 14 BP+\frac 13 CP \cong AB$

.
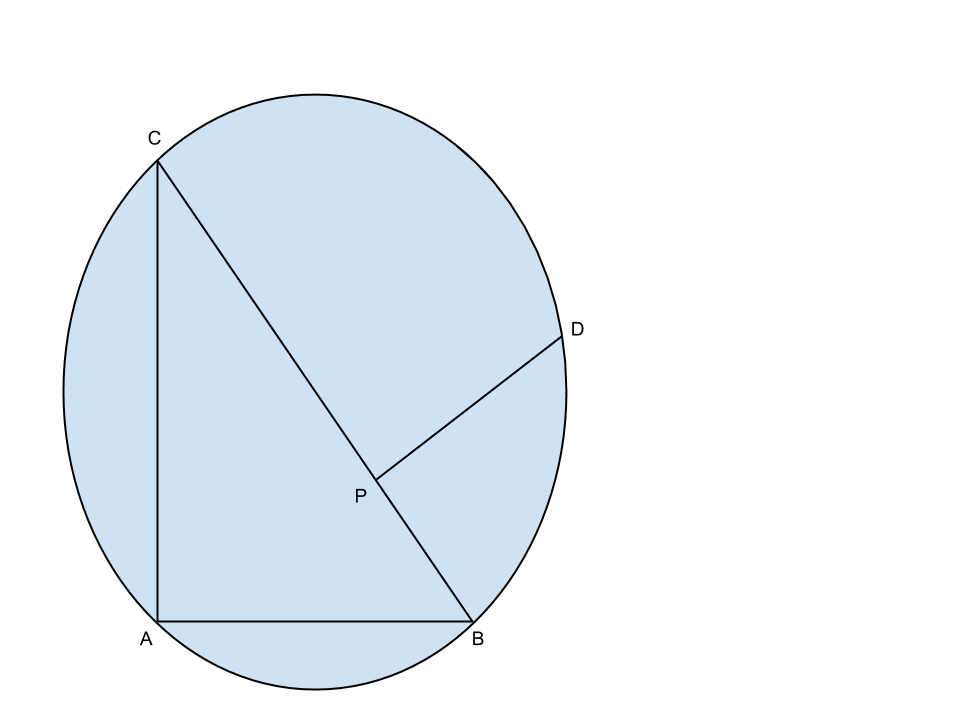
Condotta la circonferenza circoscritta al triangolo $ABC$ , sia $PD$ la semicorda, esterna al triangolo $ABC$ , perpendicolare a $BC$ . Determinare la lunghezza del perimetro e l’area del quadrilatero $ABDC$ .

Svolgimento

Poniamo $AC=x$ , così abbiamo:

$AB=7a$

$BC=x+a$ .

Utilizziamo Pitagora:

$BC^2=AC^2+AB^2$

$(x+a)^2=x^2+49a^2$

$x^2+2ax+a^2=x^2+49a^2$

$2ax=48a^2$

$x=24a$

$AC=24a$

$BC=25a$

Ora poniamo $BP=y$ , quidni avremo:

$PC = 25a - y$ .

Dalla relazione della traccia ricaviamo l’incognita:

$\frac x4 + \frac 13 (25a - x) = 7a$

$3y + 100a- 4y = 84a$

$x = 16a$

$BP = 16a$ ,

$PC=9a$ .

Circoscrivendo una circonferenza al triangolo, si nota subito che BC risulterà proprio il diametro della circonferenza, e di conseguenza avremo 2 triangoli rettangoli, ABC e BDC.

Ricaviamo quindi, con Euclide, tutti i dati che ci servono:

$DB=\sqrt {BP \cdot BC}=\sqrt {16a \cdot 25a}=20a$