Siano ![]() e
e ![]() le funzioni definite da
le funzioni definite da ![]() e
e ![]() .
.
Sia ![]() . Per quali valori di
. Per quali valori di ![]() la funzione
la funzione ![]() presenta, nell’intervallo chiuso
presenta, nell’intervallo chiuso ![]() il minimo e il massimo assoluti? Si illustri il ragionamento seguito.
il minimo e il massimo assoluti? Si illustri il ragionamento seguito.
![]()
![]()
![]()
e inoltre
![]() .
.
Calcoliamo la derivata di ![]() :
:
![]() .
.
Si nota dal grafico precedente che
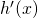 è negativo per
è negativo per ![Rendered by QuickLaTeX.com \x \in [\frac 12; x_0]](https://www.matebook.it/wp-content/ql-cache/quicklatex.com-7e3e06334d62935e3e15fe169cb83f50_l3.png) ,
,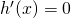 per
per 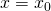 ,
,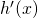 è positivo per
è positivo per ![Rendered by QuickLaTeX.com \x \in [ x_0;1]](https://www.matebook.it/wp-content/ql-cache/quicklatex.com-71aff1e5ce2b908792756c6d33852d70_l3.png) .
.
Pertanto possiamo affermare che ![]() è un punto di minimo assoluto e il massimo assoluto si avrà in uno dei due estremi, e quindi, per quanto detto prima, per
è un punto di minimo assoluto e il massimo assoluto si avrà in uno dei due estremi, e quindi, per quanto detto prima, per ![]() .
.
Altri esercizi simili
(Questa pagina è stata visualizzata da 11 persone)