Oggetto: EserciziCorpo del messaggio:
con una certa urgenza per favore
Individua il vertice C di un triangolo isoscele di base AB con 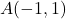 e
e 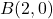 , sapendo che l’altezza relativa ad AB misura
, sapendo che l’altezza relativa ad AB misura 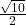 .
.
Per trovare le coordinate del punto C, basterà imporre l’uguaglianza tra la distanza dello stesso punto C col punto medio di AB e il valore datoci dalla traccia.
![]()
Imponendo che 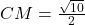 e che
e che 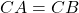 , otteniamo il sistema, considerando che C abbia coordinate
, otteniamo il sistema, considerando che C abbia coordinate 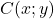 :
:
![Rendered by QuickLaTeX.com \[\begin{cases} (x+1)^2+(y-1)^2=(x-2)^2+(y-0)^2 \\ (x-\frac 12)^2+(y-\frac 12)^2=\frac {10}{4} \end{cases}\]](https://www.matebook.it/wp-content/ql-cache/quicklatex.com-fc79f01cd932c2135ca4d0a0751014f5_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} x^2+2x+1+y^2-2y+1=x^2-4x+4+y^2 \\ x^2-x+\frac 14+y^2-y+\frac 14=\frac {10}{4} \end{cases}\]](https://www.matebook.it/wp-content/ql-cache/quicklatex.com-abcdcbead8a25ce98e4c99f14d130eef_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} 6x-2y=+2 \\ x^2-x+y^2-y=2 \end{cases}\]](https://www.matebook.it/wp-content/ql-cache/quicklatex.com-d5c053283c577c1c41d0f6fe1162ce2e_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} y=3x-1 \\ x^2-x+(3x-1)^2-(3x-1)=2 \end{cases}\]](https://www.matebook.it/wp-content/ql-cache/quicklatex.com-efdf05ca212da08d569559c2e5e5bc61_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} y=3x-1 \\ x^2-x+9x^2-6x+1-3x+1=2 \end{cases}\]](https://www.matebook.it/wp-content/ql-cache/quicklatex.com-f7101813a3a631304c3132f5a84f035b_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} y=3x-1 \\ 10x^2-10x=0 \end{cases}\]](https://www.matebook.it/wp-content/ql-cache/quicklatex.com-92151d64149d955e079d73c74b13abe1_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} y=3x-1 \\ x(x-1)=0 \end{cases}\]](https://www.matebook.it/wp-content/ql-cache/quicklatex.com-a138cd31e5f94ceee133e6b7eabb0156_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} y=3x-1 \\ x_1=0 \quad \lor \quad x_2=1 \end{cases}\]](https://www.matebook.it/wp-content/ql-cache/quicklatex.com-203c7f152ca5a44bc8a903fbac9c92b2_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} y_1=-1 \quad \lor \quad y_2=2 \\ x_1=0 \quad \lor \quad x_2=1 \end{cases}\]](https://www.matebook.it/wp-content/ql-cache/quicklatex.com-2a4221960714b8eec687c43f874f5e1e_l3.png)
Quindi ci sono due possibili coordinate per il punto C:
![]()
(Questa pagina è stata visualizzata da 110 persone)
