Oggetto: Equazione e disequazione irrazionale
Corpo del messaggio:
![Rendered by QuickLaTeX.com \[\begin{cases} -x-3 \geq 0 \\ x^2-5x \geq 0 \\ -x-3<x^2-5x\end{cases}\]](https://www.matebook.it/wp-content/ql-cache/quicklatex.com-eb1fbf324d43efbff8ea3852c6c0130d_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} x \leq -3 \\ x \leq 0 \quad \lor \quad x \geq 5 \\ x^2-4x+3>0\end{cases}\]](https://www.matebook.it/wp-content/ql-cache/quicklatex.com-d1723bbf424f8b288edb559633138ca7_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} x \leq -3 \\ x \leq 0 \quad \lor \quad x \geq 5 \\ (x-3)(x-1)>0\end{cases}\]](https://www.matebook.it/wp-content/ql-cache/quicklatex.com-70418848c7908c38de8a754c8f59e35b_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} x \leq -3 \\ x \leq 0 \quad \lor \quad x \geq 5 \\ x < 1 \quad \lor \quad x > 3\end{cases}\]](https://www.matebook.it/wp-content/ql-cache/quicklatex.com-78cddb0d6ae6ab0ed2e8e1562955e0a3_l3.png)
Mettendo a sistema le tre soluzioni, notiamo che la disequazione è verificata per:
![]()
.
![]()
![Rendered by QuickLaTeX.com \[\begin{cases}5-2x \geq 0 \\ x+1 \geq 0 \\ 5-2x=x+1 \end{cases}\]](https://www.matebook.it/wp-content/ql-cache/quicklatex.com-18501898611b63e99b378e14168aac2c_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases}x \leq \frac 52 \\ x \geq -1 \\ 3x=4 \end{cases}\]](https://www.matebook.it/wp-content/ql-cache/quicklatex.com-ac5fa65567d45a68172c98953de9856f_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases}-1 \leq x \leq \frac 52 \\ x=\frac 43 \end{cases}\]](https://www.matebook.it/wp-content/ql-cache/quicklatex.com-bae1b91071ae4e4ac646eb1acbb87b4c_l3.png)
La soluzione ![]() è accettabile.
è accettabile.
(Questa pagina è stata visualizzata da 163 persone)
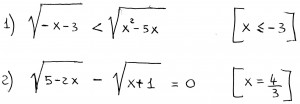
Nel secondo esercizio del tipo
radice n-esima di f(x)= radice n-esima di g(x)
è obbligatorio mettere le due condizioni di esistenza dei radicali? Una delle due non è implicita nella terza condizione del sistema?
E’ corretto oppure no quanto detto?
Grazie
Dipende dall’indice della radice.
Se l’indice è pari bisogna imporre le condizioni di esistenza.
Se l’indice è dispari non vi è l’obbligo.