Oggetto: Equazioni con valori assoluti
Corpo del messaggio:
Risposta dello staff
Dato che ![]() è sempre negativo, per qualsiasi x, basterà studiare solo 2 casi:
è sempre negativo, per qualsiasi x, basterà studiare solo 2 casi:
![Rendered by QuickLaTeX.com \[\begin {cases} 4x+2 \geq 0 \\ 4x+2 = x^2+2 \end{cases} \quad \quad \begin {cases} 4x+2 < 0 \\ -4x-2 = x^2+2 \end{cases}\]](https://www.matebook.it/wp-content/ql-cache/quicklatex.com-d532adb91c0b0fa7a0222f660f3a5657_l3.png)
![Rendered by QuickLaTeX.com \[\begin {cases} x \geq -\frac 12 \\ x^2-4x=0 \end{cases} \quad \quad \begin {cases} x < -\frac 12 \\ x^2+4x+4=0 \end{cases}\]](https://www.matebook.it/wp-content/ql-cache/quicklatex.com-1271427c2f1c3577e00c9c5ad0f000bc_l3.png)
![Rendered by QuickLaTeX.com \[\begin {cases} x \geq -\frac 12 \\ x=0 \quad \lor \quad x=4 \end{cases} \quad \quad \begin {cases} x < -\frac 12 \\ x=-2 \end{cases}\]](https://www.matebook.it/wp-content/ql-cache/quicklatex.com-604516902a232bb05c9c4611b00ddda3_l3.png)
Nel primo sistema avremo un’equazione spuria, e nel secondo il quadrato di un binomio. Sono tutte e 3 soluzioni accettabili.
Senza fare grossi calcoli ci accorgiamo che il fattore di sinistra sarà sempre positivo, mentre quello di destra sarà sempre negativo…
Riscriviamo in questo modo:
![]()
![]()
Da qui avremo che il primo fattore può essere uguale a 0 per ![]() , mentre il secondo non sarà mai uguale a 0 per nessun valore della x.
, mentre il secondo non sarà mai uguale a 0 per nessun valore della x.
Qui dovremmo studiare 3 sistemi, ma essendo la differenza uguale a 0, i sistemi per ![]() e per
e per ![]() coincideranno:
coincideranno:
![Rendered by QuickLaTeX.com \[\begin{cases} x < -3 \quad \lor \quad x>2 \\ \frac {2}{x+3}-\frac {3}{x-2} =0 \end{cases} \quad \quad \begin{cases} -3 < x<2 \\ \frac {2}{x+3}+\frac {3}{x-2} =0 \end{cases}\]](https://www.matebook.it/wp-content/ql-cache/quicklatex.com-99fc3a74b200716f532a9811a34d9d22_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} x < -3 \quad \lor \quad x>2 \\ 2x-4-3x-9 =0 \end{cases} \quad \quad \begin{cases} -3 < x<2 \\2x-4+3x+9=0 \end{cases}\]](https://www.matebook.it/wp-content/ql-cache/quicklatex.com-f926a4e91d29b9d64732ab40671b445b_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} x < -3 \quad \lor \quad x>2 \\ -x =13 \end{cases} \quad \quad \begin{cases} -3 < x<2 \\5x=-5 \end{cases}\]](https://www.matebook.it/wp-content/ql-cache/quicklatex.com-99e8fafdff49389cfe3b972716d3c537_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} x < -3 \quad \lor \quad x>2 \\ x =-13 \end{cases} \quad \quad \begin{cases} -3 < x<2 \\x=-1 \end{cases}\]](https://www.matebook.it/wp-content/ql-cache/quicklatex.com-045b3ebfce5a0e96e55432e84cdacb81_l3.png)
Soluzioni entrambe accettabili.
(Questa pagina è stata visualizzata da 251 persone)
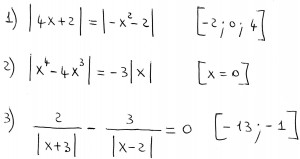
In merito al primo esercizio vorrei sapere se è indifferente mettere il segno di uguaglianza nelle disequazioni dei sistemi, cioè scrivere nel primo sistema:
4x+2>0
e nel secondo:
4x+2<=0.
Distinti saluti.
Assolutamente indifferente.
In merito al primo esercizio, essendo un’equazione del tipo:
Modulo di f(x) = Modulo di g(x)
si poteva anche risolvere semplicemente imponendo
f(x)=g(x) e f(x)= – g(x)
senza mettere a sistema le condizioni 4x+2>=0 e 4x+2<0.
Grazie
Assolutamente si.
Ho fatto la solita discussione standard che si fa per i valori assoluti, perchè comunque questo risulta un caso particolare.
L’equazione n.1 si poteva risolvere anche elevando ambo i membri al quadrato essendo due quantità positive?
Grazie
Si… Ma onde evitare di affrontare equazioni di quarto grado, sarebbe preferibile cercare di tenere il più basso possibile il grado (questo è un mero consiglio, poi ognuno è libero di svolgere l’esercizio in altro modo).
Quello che proponiamo non è mai l’unica soluzione all’esercizio, ma una spiegazione di un possibile svolgimento.