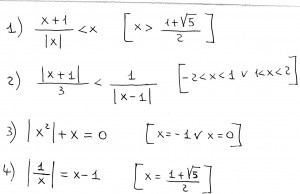Oggetto: Equazioni e disequazioni con valori assoluti
Corpo del messaggio:
Risposta dello staff
Distingueremo due casi:
![Rendered by QuickLaTeX.com \[\begin{cases} x>0 \\ \frac {x+1}{x}<x \end{cases} \quad \quad \begin{cases} x<0 \\ -\frac {x+1}{x}<x \end{cases}\]](https://www.matebook.it/wp-content/ql-cache/quicklatex.com-147efa5b5e760bf73bbc3153533cba3f_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} x>0 \\ \frac {x+1}{x}-x<0 \end{cases} \quad \quad \begin{cases} x<0 \\ -\frac {x+1}{x}-x<0 \end{cases}\]](https://www.matebook.it/wp-content/ql-cache/quicklatex.com-0ceb91305b3c8f03d05b9fe6b01e2454_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} x>0 \\ x+1-x^2<0 \end{cases} \quad \quad \begin{cases} x<0 \\ x+1+x^2<0 \end{cases}\]](https://www.matebook.it/wp-content/ql-cache/quicklatex.com-a53fc027170fc8b997c90ac1e7f4d11e_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} x>0 \\ x^2-x-1>0 \end{cases} \quad \quad \begin{cases} x<0 \\ \Delta <0 \end{cases}\]](https://www.matebook.it/wp-content/ql-cache/quicklatex.com-49c9924991daa9e71fb2ec6433ddf468_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} x>0 \\ x< \frac {1-\sqrt 5}{2} \quad \lor \quad x>\frac {1+\sqrt 5}{2} \end{cases}\]](https://www.matebook.it/wp-content/ql-cache/quicklatex.com-4ce56cc3f2133e34183bce1920f6cad3_l3.png)
Quindi la soluzione sarà: ![]() .
.
Distingueremo tre casi
![Rendered by QuickLaTeX.com \[\begin{cases} x\leq -1 \\ \frac {-x-1}{3}<\frac {1}{1-x} \end{cases} \quad \quad \begin{cases} -1<x<1 \\ \frac {x+1}{3}<\frac {1}{1-x} \end{cases} \quad \quad \begin{cases} x > 1 \\ \frac {x+1}{3}<\frac {1}{x-1} \end{cases}\]](https://www.matebook.it/wp-content/ql-cache/quicklatex.com-bb8c7a823b8d09a38061d4e98e6715d3_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} x\leq -1 \\ \frac {-x-1}{3}-\frac {1}{1-x}<0 \end{cases} \quad \quad \begin{cases} -1<x<1 \\ \frac {x+1}{3}-\frac {1}{1-x}<0 \end{cases} \quad \quad \begin{cases} x > 1 \\ \frac {x+1}{3}-\frac {1}{x-1}<0 \end{cases}\]](https://www.matebook.it/wp-content/ql-cache/quicklatex.com-4b3dc809e796774472cdb5c102722e23_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} x\leq -1 \\ \frac {-x+x^2-1+x-3}{3(1-x)}<0 \end{cases} \quad \quad \begin{cases} -1<x<1 \\ \frac {x-x^2+1-x-3}{3(1-x)}<0 \end{cases} \quad \quad \begin{cases} x > 1 \\ \frac {x^2-x-x+1}{3(x-1)}<0 \end{cases}\]](https://www.matebook.it/wp-content/ql-cache/quicklatex.com-d3eea5631c9d3bac7031c36f68347fa6_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} x\leq -1 \\ x^2<4 \end{cases} \quad \quad \begin{cases} -1<x<1 \\ -x^2-2<0 \end{cases} \quad \quad \begin{cases} x > 1 \\ x^2-4<0 \end{cases}\]](https://www.matebook.it/wp-content/ql-cache/quicklatex.com-5fe589a10eaf5d14af7e44e58588e96e_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} x\leq -1 \\ -2<x<2 \end{cases} \quad \quad \begin{cases} -1<x<1 \\ \forall x \in R \end{cases} \quad \quad \begin{cases} x > 1 \\ -2<x<2 \end{cases}\]](https://www.matebook.it/wp-content/ql-cache/quicklatex.com-3a74300e7f036543cad2a45cc22d75b7_l3.png)
Le soluzioni saranno:
Unendo tutto avremo ![]() con
con ![]() .
.
Essendo ![]() sempre positivo, possiamo eliminare il valore assoluto e risolvere l’equazione semplice
sempre positivo, possiamo eliminare il valore assoluto e risolvere l’equazione semplice
![]()
![]()
![]()
![]()
Distinguiamo due casi:
![Rendered by QuickLaTeX.com \[\begin{cases} x>0 \\ \frac {1}{x}=x-1 \end{cases} \quad \quad \begin{cases} x<0 \\ \frac {1}{x}=1-x \end{cases}\]](https://www.matebook.it/wp-content/ql-cache/quicklatex.com-3075cb8bcdc07e1c56db72726d09efe1_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} x>0 \\ x^2-x-1=0 \end{cases} \quad \quad \begin{cases} x<0 \\ x^2-x+1=0 \end{cases}\]](https://www.matebook.it/wp-content/ql-cache/quicklatex.com-0b0317589eeeab49ae4c90a46d50c6dd_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} x>0 \\ x= \frac {1 \pm \sqrt 5}{2} \end{cases} \quad \quad \begin{cases} x<0 \\ \Delta<0 \end{cases}\]](https://www.matebook.it/wp-content/ql-cache/quicklatex.com-4927e962e334f042eeac13353db127e1_l3.png)
Nel primo sistema avremo una sola soluzione accettabile, ovvero ![]() .
.
(Questa pagina è stata visualizzata da 118 persone)