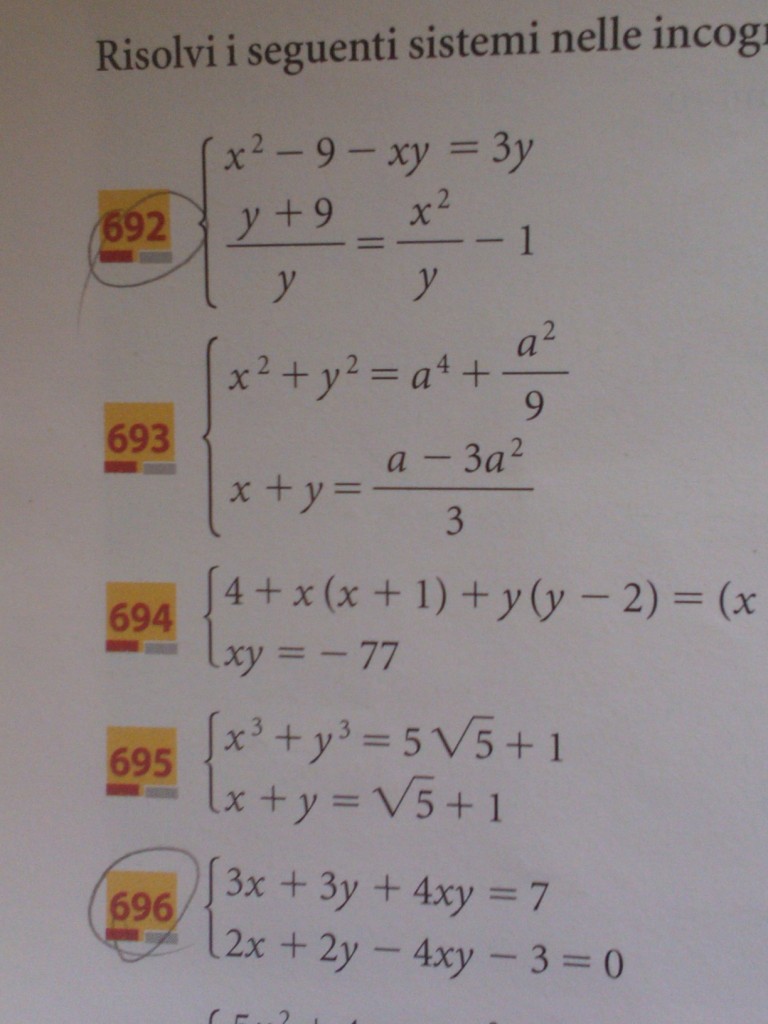Oggetto: equazioni n 692- 696
Corpo del messaggio:
Risposta dello staff
692)
![Rendered by QuickLaTeX.com \[\begin{cases} x^2-9-xy=3y \\ \frac {y+9}{y} = \frac {x^2}{y}-1\end{cases}\]](https://www.matebook.it/wp-content/ql-cache/quicklatex.com-6ac8ea03879c7212d75d50f62e09d596_l3.png)
Imponendo che ![]() :
:
![Rendered by QuickLaTeX.com \[\begin{cases} x^2-9-xy-3y=0 \\ y+9 = x^2-y\end{cases}\]](https://www.matebook.it/wp-content/ql-cache/quicklatex.com-8554ac55496c574f5cec055380a89931_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} x^2-9-xy-3y=0 \\ x^2-9-2y=0\end{cases}\]](https://www.matebook.it/wp-content/ql-cache/quicklatex.com-32b0652a6141d4a1077e40f43f4c684c_l3.png)
Sottraendo le due equazioni otteniamo:
![Rendered by QuickLaTeX.com \[\begin{cases} -xy-y=0 \\ x^2-9-2y=0\end{cases}\]](https://www.matebook.it/wp-content/ql-cache/quicklatex.com-61d9197f59576c467ed2598c014312bd_l3.png)
Avendo imposto che ![]() , otteniamo:
, otteniamo:
![Rendered by QuickLaTeX.com \[\begin{cases} x=-1 \\ 2y=-8\end{cases}\]](https://www.matebook.it/wp-content/ql-cache/quicklatex.com-c012d71dd15d953ce01ac9e86a246018_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} x=-1 \\ y=-4\end{cases}\]](https://www.matebook.it/wp-content/ql-cache/quicklatex.com-72610181dd49e4ab9b57449290ecba55_l3.png)
696)
![Rendered by QuickLaTeX.com \[\begin{cases} 3x+3y+4xy=7 \\ 2x+2y-4xy-3=0\end{cases}\]](https://www.matebook.it/wp-content/ql-cache/quicklatex.com-8fc18355fc645c283d4b3cea679beb16_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} 3x+3y+4xy=7 \\ 5x+5y=10\end{cases}\]](https://www.matebook.it/wp-content/ql-cache/quicklatex.com-5323acf1517328138ad9adbe13e733e3_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} 3x+3y+4xy=7 \\ x=2-y\end{cases}\]](https://www.matebook.it/wp-content/ql-cache/quicklatex.com-3a14f451820779458b0b136a556c1a66_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} 3(2-y)+3y+4(2-y)y=7 \\ x=2-y\end{cases}\]](https://www.matebook.it/wp-content/ql-cache/quicklatex.com-94ad780e7a66b845b5a5b73e53eec5cd_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} 6-3y+3y+8y-4y^2-7=0 \\ x=2-y\end{cases}\]](https://www.matebook.it/wp-content/ql-cache/quicklatex.com-12034d0c20be105291414b9d6b77309e_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} 4y^2-8y+1=0 \\ x=2-y\end{cases}\]](https://www.matebook.it/wp-content/ql-cache/quicklatex.com-b726e1d283b8db0464b16ea852a7a6ce_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} y_{\frac 12}= \frac {8 \pm \sqrt {64-16}}{8}=\frac {8 \pm 4\sqrt {3}}{8} \\ x=2-y\end{cases}\]](https://www.matebook.it/wp-content/ql-cache/quicklatex.com-e5d6597739e5b5ae3d2840412409e453_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} y_{\frac 12}=1 \pm \frac 12 \sqrt 3 \\ x=2-y\end{cases}\]](https://www.matebook.it/wp-content/ql-cache/quicklatex.com-9977f3ba9901afc54b6c1de861c4dd0f_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} y_1=1 - \frac 12 \sqrt 3 \quad y_2=1 + \frac 12 \sqrt 3 \\ x_1=1+\frac 12 \sqrt 3 \quad x_2=1-\frac 12 \sqrt 3 \end{cases}\]](https://www.matebook.it/wp-content/ql-cache/quicklatex.com-87f1728471a693262e4be5b50cf41b78_l3.png)
(Questa pagina è stata visualizzata da 53 persone)