Leandro scrive: Esercizi sulla retta

Pubblicato il da Lo Staff2 commenti
0

Oggetto: Esercizi sulla retta

Corpo del messaggio:

img057

 

Risposta dello staff

1)

Sappiamo per certo che il triangolo AOB è retto. Calcoliamo le coordinate dei punti in funzione di k:

A\left(\frac {5-k}{k};0\right)

B\left(0; 5-k\right)

Calcoliamo l’area e imponiamo che sia uguale a 8:

\frac {\frac {5-k}{k} \cdot (5-k)}{2}=8

(5-k)^2=16k

k^2-10k+25-16k=0

k^2-26k+25=0

(k-1)(k-25)=0

da cui avremo le due soluzioni, entrambe accettabili:

k=1 \quad \lor \quad k=25.

2) Escludiamo prima il caso in cui le rette siano parallele, ovvero quando le due rette hanno lo stesso coefficiente angolare:

\frac {2}{k-3}=-\frac {1}{k-1}

2k-2=-k+3

3k=1

k=\frac 13

Escludendo questo valore, per il quale le rette non si incontreranno mai, otteniamo:

\begin{cases} 2x-(k-3)y+8k-2=0 \\ x+(k+1)y+k=0\end{cases}

\begin{cases} -2y(k+1)-2k-(k-3)y+8k-2=0 \\ x=-(k+1)y-k\end{cases}

\begin{cases} -2ky-2y-2k-ky+3y+8k-2=0 \\ x=-(k+1)y-k\end{cases}

\begin{cases} -3yk+y+6k-2=0 \\ x=-(k+1)y-k\end{cases}

\begin{cases} y(1-3k)=2(1-3k) \\ x=-(k+1)y-k\end{cases}

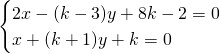
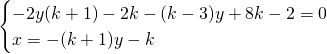
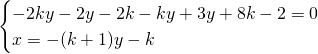
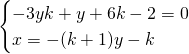
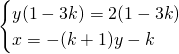
Avendo imposto che k \neq \frac 13 otteniamo:

\begin{cases} y=2 \\ x=-(k+1)y-k\end{cases}

\begin{cases} y=2 \\ x=-2k-2-k=-2-3k\end{cases}

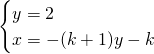
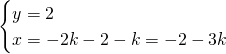
3)

La retta r è parallela alla retta t, di conseguenza sarà del tipo:

y=2x+q

Calcoliamo q imponendo il passaggio per A:

-4=-10+q

q=6

r: y=2x+6

La retta s è perpendicolare alla retta t, di conseguenza sarà del tipo:

y=-\frac 12 x+q

Calcoliamo q imponendo il passaggio per A:

-4=\frac 52+q

q=-\frac {13}{2}

s: y=-\frac 12 x-\frac {13}{2}

Troviamo le coordinate di B:

\begin{cases} y=2x+1 \\ y=-\frac 12 x-\frac {13}{2}\end{cases}

\begin{cases} y=2x+1 \\ 2x+1=-\frac 12 x-\frac {13}{2}\end{cases}

\begin{cases} y=2x+1 \\ 4x+2=- x-13\end{cases}

\begin{cases} y=2x+1 \\ 5x=-15\end{cases}

\begin{cases} y=-5 \\ x=-3\end{cases}

B(-3;-5)

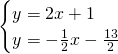
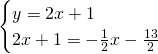
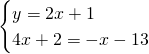
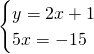
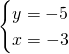
Troviamo le coordinate degli altri 2 punti:

C(0;1)

D(0;6)

Per costruzione sappiamo che r e t sono parallele e s e t sono perpendicolari.

Di conseguenza, essendo CD non perpendicolare a r (o a t)  questo sarà un trapezio rettangolo.

Calcoliamo l’area, trovando le lunghezze dei lati:

AB=\sqrt{(-5+3)^2+(-4+5)^2}=\sqrt{4+1}=\sqrt 5

AD=\sqrt{(-5)^2+(-4-6)^2}=\sqrt{25+100}=5\sqrt 5

CB=\sqrt{(3)^2+(1+5)^2}=\sqrt{9+36}=3\sqrt 5

A= \frac {(AD+BC) \cdot AB}{2}=\frac {8\sqrt 5 \cdot \sqrt 5}{2}=20

 

(Questa pagina è stata visualizzata da 100 persone)

2 pensieri riguardo “Leandro scrive: Esercizi sulla retta”

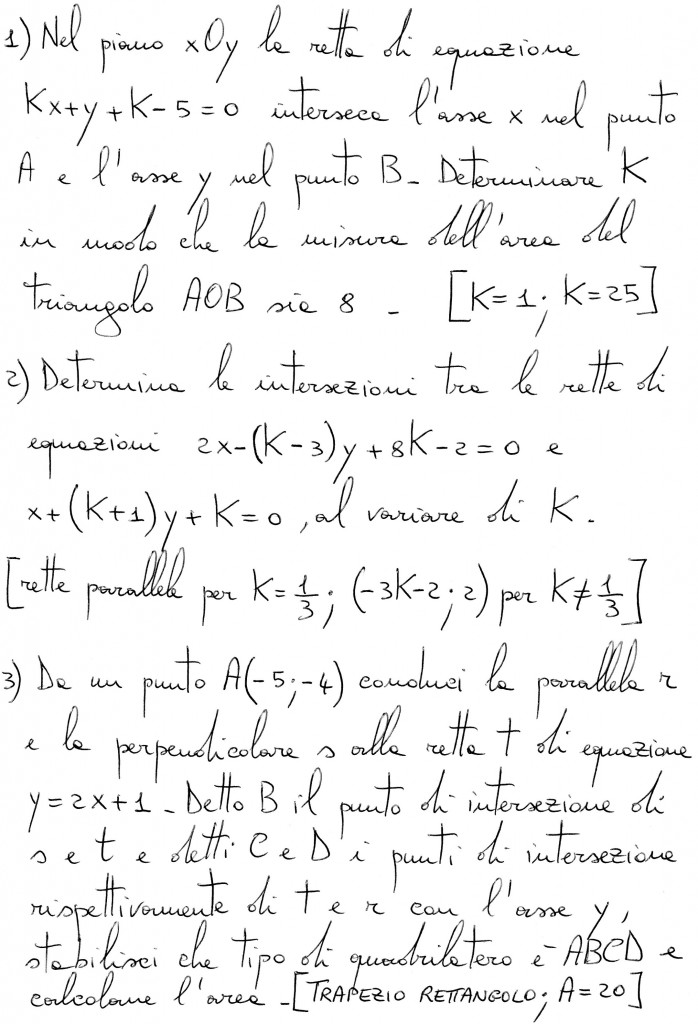
  1. In merito all’esercizio n.1, nel calcolo dell’area del triangolo non ci vuole il modulo alle misure dei segmenti OA e OB, cioè modulo di 5-k diviso k per modulo di 5-k.

    Grazie

    1. Si. In realtà lo studio si limiterebbe solo al calcolo del modulo di k, visto che il prodotto dei moduli equivale al modulo del prodotto.
      Chiedo scusa per aver saltato il passaggio, avendo dato per scontato che, non ammettendo soluzioni accettabili, non fosse da considerare.

Lascia un commento