Oggetto: la circonferenza
Corpo del messaggio:
Dato il triangolo di vertici a(-4; 3), b(-6;-3),c(0;-5), determina le equazioni delle tangenti alka crf perpendicolari alla retta x-2y-9=0.
Urgente Grazie per l’al’aiuto!!
Non è chiarissima la traccia, ma credo che la circonferenza passi per i 3 vertici del triangolo. Di conseguenza avremo:
![]()
Ricaviamo l’equazione con il passaggio per i 3 punti:
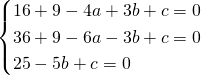
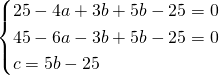
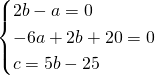
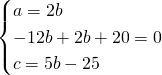
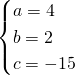
L’equazione della circonferenza sarà quindi:
![]() .
.
Le rette perpendicolari alla retta data saranno del tipo:
![]()
Andando a sostituire nell’equazione della circonferenza e poi ponendo il ![]() , otterremo il risultato cercato:
, otterremo il risultato cercato:
![]()
![]()
![]()
![]()
![]()
![]()
Poniamo il ![]() , e avremo:
, e avremo:
![]()
![]()
e di conseguenza le due rette cercate saranno:
![]()
![]()
(Questa pagina è stata visualizzata da 59 persone)