Oggetto: Fasci di rette
Corpo del messaggio:
Risposta dello staff
1)
a) ![]()
![]()
Le due rette generatrici saranno:
![]() e
e ![]()
Il centro del fascio sarà:
![]()
Per il verso, analogamente all’altro esercizio che avevi richiesto, basterà assegnare dei valori particolari a k. Se passa per l’origine avremo ![]() e di conseguenza ruoterà in senso orario.
e di conseguenza ruoterà in senso orario.
b) ![]()
![]()
Le due rette generatrici saranno:
![]() e
e ![]()
Il centro del fascio sarà:
![]()
Per il verso, analogamente all’altro esercizio che avevi richiesto, basterà assegnare dei valori particolari a k. Se passa per l’origine avremo ![]() e di conseguenza ruoterà in senso antiorario.
e di conseguenza ruoterà in senso antiorario.
2)
Una generica retta che passa per C avrà coordinate
![]()
con
![]()
e quindi:
![]() .
.
Troviamo le coordinate dei tre vertici del triangolo:
![]()
![]()
Per trovare il terzo vertice mettiamo a sistema:
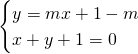
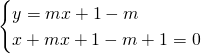
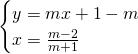
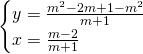
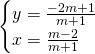
![]()
Per calcolare l’area possiamo considerare come base il segmento che giace sulla retta ![]() , e come altezza la differenza di ascisse tra i punti, così da ottenere:
, e come altezza la differenza di ascisse tra i punti, così da ottenere:
![]()
![]()
![]()
![]()
![]()
Studiamo i due casi:
![]()
che non ammetterà soluzioni
![]()
![]()
da cui avremo:
![]()
Andando a sostituire nella retta richiesta questi valori otteniamo le due rette appartenenti al fascio proprio:
![]() e
e ![]()
3)
![]()
![]()
![]()
Il centro del fascio sarà:
![]()
e di conseguenza ricaviamo il valore di m della retta che passera per quel punto:
![]()
![]()
La retta sarà:
![]()
E questa è proprio una delle rette generatrici del fascio, ovvero quella che si ottiene per ![]()
(Questa pagina è stata visualizzata da 116 persone)
