Giuseppe scrive: Equazione di grado superiore al secondo

Oggetto: Equazione di grado superiore al secondo

Corpo del messaggio:

Essendo a sotto una radice di indice pari, assumiamo subito che a debba essere positivo.

Se $a=0$ , l’equazione si ridurrebbe ad essere un’equazione spuria di secondo grado:

$x^2-x=0$

$x(x-1)=0$

da cui le soluzioni saranno:

$x=0 \quad \wedge \quad x=1$

Analizziamo invece il caso generico $a>0$ :

$\sqrt a(x^3-1)+x(a-\sqrt a+1)(x-1)=0$

$\sqrt a(x-1)(x^2+x+1)+x(a-\sqrt a+1)(x-1)=0$

$(x-1)(\sqrt a x^2+\sqrt a x+\sqrt a+ax-\sqrt ax+x)=0$

$(x-1)(\sqrt a x^2+ax+x+\sqrt a)=0$

Il primo fattore sarà verificato per $x=1$ .

Andiamo a calcolare l’equazione di secondo grado:

$x_{\frac 12}=\frac {-a-1 \pm \sqrt {a^2+2a+1-4a}}{2\sqrt a}=\frac {-a-1 \pm \sqrt {(a-1)^2}}{2\sqrt a}=\frac {-a-1 \pm (a-1)}{2\sqrt a}$

$x_1=\frac {-a-1 -a+1}{2\sqrt a}=-\sqrt a$

$x_2=\frac {-a-1 +a-1}{2\sqrt a}=-\frac{1}{\sqrt a}$

(Questa pagina è stata visualizzata da 165 persone)

3 pensieri riguardo “Giuseppe scrive: Equazione di grado superiore al secondo”

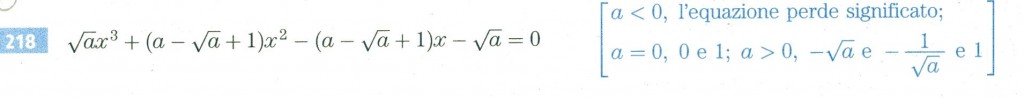
grazie per la disponibilità ma non ho ben compreso il passaggio sotto a > 0. in attesa di ulteriori chiarimenti vi ringrazio.

Edo ha detto:

24 Aprile 2014 alle 08:53

Spiego meglio i passaggi:

prima di tutto ho messo a fattor comune parziale radice di a per il primo e il quarto termine e i fattori in parentesi tra il secondo ed il terzo.

Successivamente ho scomposto il binomio x^3-1.

In seguito ho messo a fattor comune totale x-1, comune ad entrambi i fattori.

Spero di aver chiarito i dubbi!!!

Accedi per rispondere

Mi siete stato di aiuto. Grazie allo staff di MATEBOOK.

Devi essere connesso per inviare un commento.

Matebook