Leandro scrive: Divisione tra polinomi

Pubblicato il da Lo Staff2 commenti
0

Oggetto: Divisione tra polinomi

Corpo del messaggio:

img067

 

Risposta dello staff

1)

a)

2 -b b^2 -b^3
-b -2b 3b^2 -4b^3
2 -3b 4b^2 -5b^3

Essendo il coefficiente della a nel polinomio divisore negativo, cambieremo il segno del quoziente e quindi avremo che:

(2a^3-ba^2+ab^2-b^3):(-a-b)=(-2a^2+3ab-4b^2)-5b^3

b)

3a^{n+1} -a^{2n+1} 0 9a^{n-1} -3a^{2n-1}
\frac 13 a^n a^{2n+1} 0 0 3a^{2n-1}
3a^{n+1} 0 0 9a^{n-1} 0

 

Essendo il coefficiente della a nel polinomio divisore 3, divideremo il quoziente e quindi avremo che:

(3b^4a^{n+1}-b^3a^{2n+1}+9ba^{n-1}-3a^{2n-1}):(3b-a^{n})=b^3a^{n+1}+3a^{n-1}

 

2) Sostituiamo al posto dell’incognita il valore \frac 13, e otteniamo così:

\frac {1}{81}- \frac {7}{81}+\frac{20}{27}-\frac 53+2-1=- \frac {6}{81}+\frac{20}{27}-\frac 53+2-1=

=- \frac {2}{27}+\frac{20}{27}-\frac 53+2-1=\frac{18}{27}-\frac 53+2-1=

=\frac{2}{3}-\frac 53+2-1=-1+2-1=0

(Questa pagina è stata visualizzata da 175 persone)

2 pensieri riguardo “Leandro scrive: Divisione tra polinomi”

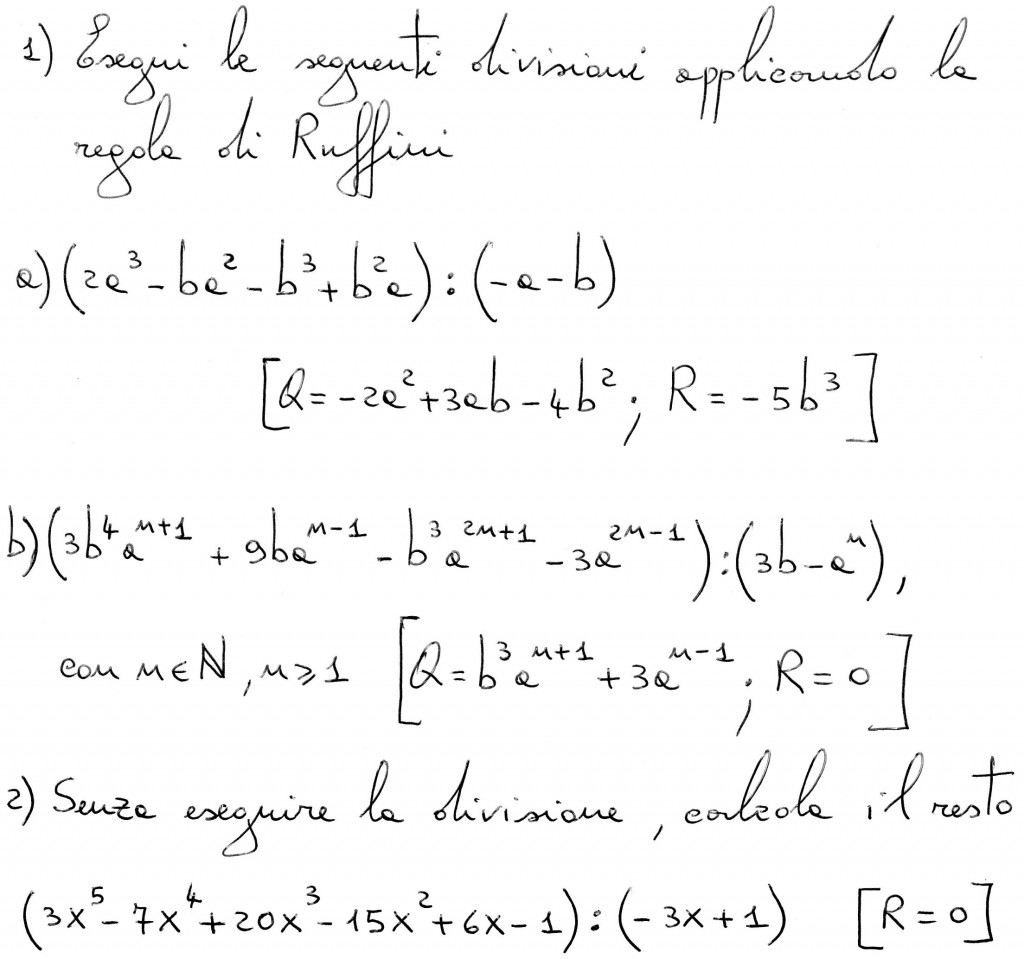
  1. In merito all’esercizio n. 2, potrebbe spiegarmi come si ottiene il valore 1/3. Si deve scrivere il divisore nella forma x-a però siccome x è negativo come viene?

    Grazie

    1. Non dovendo eseguire la divisione, ma conoscere solo il resto, basterà semplicemente studiare l’equazione -3x+1=0, da cui si ottiene x=1/3.
      Per calcolare il resto, cambiare il segno al divisore è ininfluente.

Lascia un commento