Oggetto: Circonferenza
Corpo del messaggio:
Risposta dello staff
1) Senza fare grossi calcoli basterà notare che, il diametro della più piccola circonferenza apparterrà alla retta passante per i due centri.
![]()
![]()
Facendo il disegno e tracciando la linea individuiamo tre segmenti:
- il primo sarebbe il raggio della circonferenza più piccola, di lunghezza 1.
- il secondo è il segmento che congiunge i 2 centri, di lunghezza
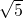 .
. - il terzo è il raggio della circonferenza più grande, di lunghezza 2.
Quindi, il diametro della circonferenza sarebbe:
![]() .
.
Il raggio si ottiene dividendo per 2.
2) per ricavare la retta t, troviamo i centri dei due fasci:
![]()
![]()
![]()
![]()
![]()
![]()
Ricaviamo la retta passante per i due punti ![]() e
e ![]() :
:
![]()
![]()
![]()
Per ricavare l’area del triangolo troviamo i due punti di intersezione della retta con gli assi coordinati:
![]()
![]()
![]()
Per definizione, in un triangolo rettangolo ortocentro, circocentro e baricentro sono allineati, ma verifichiamo con i calcoli. Per verificare che i tre punti siano allineati, calcoliamo le coordinate:
L’ortocentro sarà ovviamente l’origine, in quanto punto di intersezione delle altezze.
Il baricentro lo calcoliamo:
![]()
La retta che passa per O e G sarà:
![]()
![]()
![]()
Il circocentro, essendo l’intersezione degli assi, lo possiamo calcolare tracciando le perpendicolare ai due cateti del triangolo rettangolo nei loro punti medi.
Le due rette saranno:
![]() e
e ![]()
Quindi: ![]()
Vediamo se verifica le condizioni di passaggio:
![]()
![]()
come volevasi dimostrare.
(Questa pagina è stata visualizzata da 95 persone)
