Oggetto: problema con euclide
Corpo del messaggio:
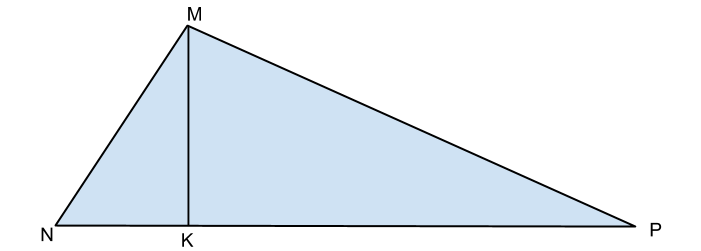
in un triangolo rettangolo l’ipotenusa misura 50a e la somma dei due cateti e l’altezza relativa all’ipotenusa misura 94a , trovare perimetro ed aria
Risposta dello staff
Per Euclide sappiamo che:
![]()
![]()
Ponendo i due cateti come incognite, ![]() , e
, e ![]() avremo:
avremo:
![]()
![]()
Per il secondo teorema di Euclide sappiamo che:
![]()
Avremo quindi il sistema:
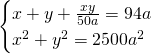
Essendo un sistema simmetrico, poniamo ![]() e
e ![]() e otteniamo:
e otteniamo:
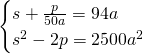
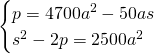
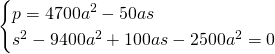
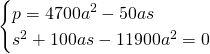
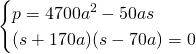
Ovviamente potremo accettare solo una soluzione e quindi:
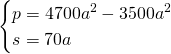
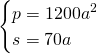
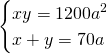
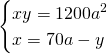

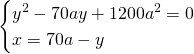
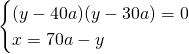
Le soluzioni saranno quindi:
![]() e
e ![]() .
.
![]()
![]()
(Questa pagina è stata visualizzata da 78 persone)