Leandro scrive: Fasci di circonferenze

Pubblicato il da Lo Staff2 commenti
0

Oggetto: Fasci di circonferenze

Corpo del messaggio:

img072

 

Esercizi svolti

A)

Troviamo subito il centro del fascio:

C\left(0;\frac{4k+3}{2}\right)

Quindi, ha sempre ascissa 0, ma l’ordinata del centro varia al variare di k.

Calcoliamo il raggio:

r=\frac 12 \sqrt{a^2+b^2-4c}=\frac 12 \sqrt{(4k+3)^2}=\frac {4k+3}{2}

Quindi, il raggio misura esattamente quanto l’ordinata del centro, e quindi tutte le circonferenze passeranno ed addirittura, saranno tangenti nell’origine.

B)

Calcolando il centro del fascio otteniamo:

C\left(2;-3\right)

Di conseguenza, variando solo il raggio e rimanendo il centro fisso per qualsiasi valore di k, queste saranno concentriche, rispetto a C.

C)

Riscriviamo meglio l’equazione:

x^2+y^2-9x+2y+5+k(x^2+y^2-x-10y+9)=0

Svolgiamo il sistema e otteniamo:

\begin{cases} x^2+y^2-9x+2y+5=0 \\ x^2+y^2-x-10y+9=0 \end{cases}

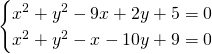
Sottraendo membro a membro otteniamo:

-8x+12y-4=0

2x-3y+1=0

Ora, mettendo a sistema la retta generatrice con una circonferenza otterremo i due punti base:

\begin{cases} x^2+y^2-9x+2y+5=0 \\ 2x-3y+1=0 \end{cases}

\begin{cases} x^2+y^2-9x+2y+5=0 \\ x=\frac {3y-1}{2} \end{cases}

\begin{cases} \frac {9y^2-6y+1}{4}+y^2-\frac 92 (3y-1)+2y+5=0 \\ x=\frac {3y-1}{2} \end{cases}

\begin{cases} 9 y^2-6y+1+4y^2-54y+18+8y+20=0 \\ x=\frac {3y-1}{2} \end{cases}

\begin{cases} 13 y^2-52y+39=0 \\ x=\frac {3y-1}{2} \end{cases}

\begin{cases} y^2-4y+3=0 \\ x=\frac {3y-1}{2} \end{cases}

\begin{cases} (y-3)(y-1)=0 \\ x=\frac {3y-1}{2} \end{cases}

\begin{cases} y_1= 3 \quad \lor \quad y_2=1 \\ x_1=4 \quad \lor \quad x_2=1 \end{cases}

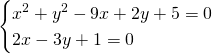
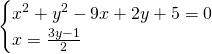
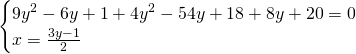
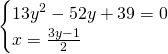
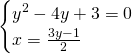
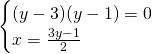
I due punti base saranno quindi:

A(4;3) e B(1;1)

D)

Riscriviamo meglio l’equazione:

x^2+y^2+2x+2y+2+k(2x-y+1)=0

Svolgiamo il sistema e otteniamo:

\begin{cases} x^2+y^2+2x+2y+2=0 \\ 2x-y+1=0 \end{cases}

\begin{cases} x^2+y^2+2x+2y+2=0 \\ y=2x+1 \end{cases}

\begin{cases} x^2+4x^2+4x+1+2x+4x+2+2=0 \\ y=2x+1 \end{cases}

\begin{cases} 5x^2+10x+5=0 \\ y=2x+1 \end{cases}

\begin{cases} x^2+2x+1=0 \\ y=2x+1 \end{cases}

\begin{cases} (x+1)^2=0 \\ y=2x+1 \end{cases}

\begin{cases} x=-1 \\ y=-1 \end{cases}

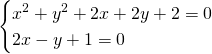
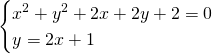
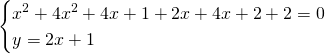
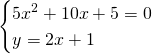
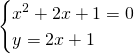
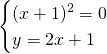
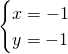
Le circonferenze saranno tangenti in T(-1;-1)

e)

Come nella seconda notiamo che il centro sarà:

C\left(-1;2\right)

e di conseguenza le circonferenze saranno concentriche con centro C.

(Questa pagina è stata visualizzata da 178 persone)

2 pensieri riguardo “Leandro scrive: Fasci di circonferenze”

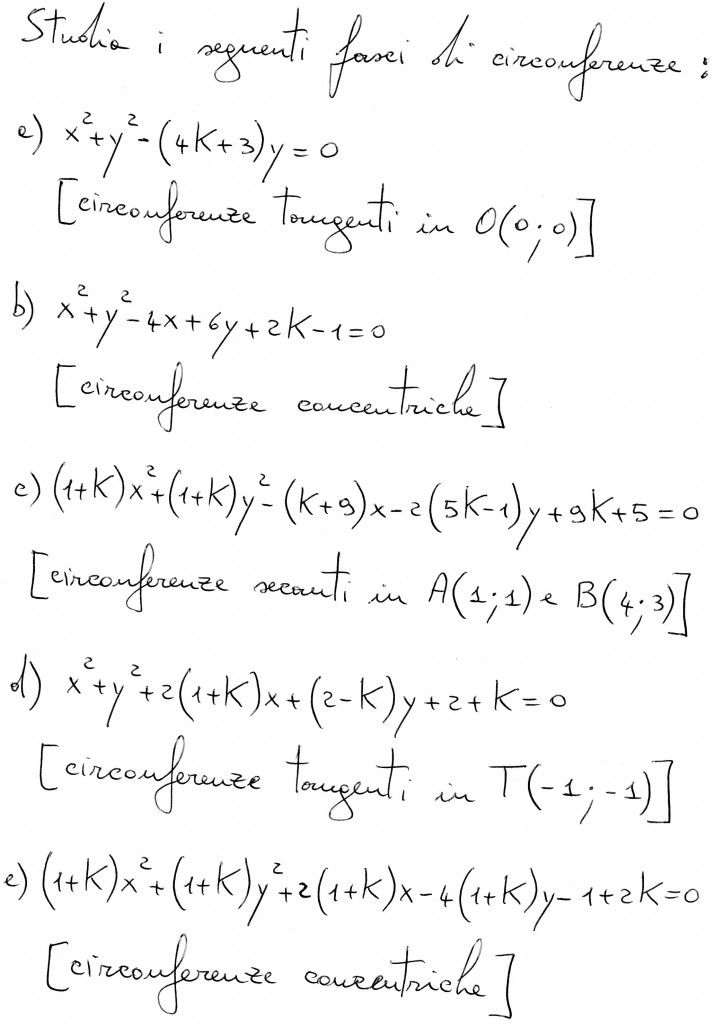
  1. Credo che i risultati dell’esercizio c siano esatti.
    Sembra che è stato commesso un errore nella seconda circonferenza generatrice. L’equazione dovrebbe essere:
    x^2+y^2-x-10y+9=0

    E’ giusto?

    Distinti saluti

Lascia un commento