Oggetto: Fasci di circonferenze
Corpo del messaggio:
Risposta dello staff
Il modo migliore per capire in che relazione sono le due circonferenze è studiare la distanza tra i due centri:
![]()
![]()
![]()
![]()
Calcoliamo la distanza tra i centri e vediamo che:
![]()
Di conseguenza, essendo la distanza tra i centri maggiore della somma dei raggi, le due circonferenze non sono secanti.
Ricaviamo l’asse radicale del fascio:
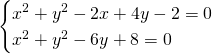
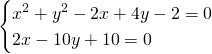
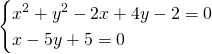
L’equazione del fascio risulta essere quindi:
![]() .
.
Ci viene chiesto di trovare per quale valore di k il centro giace sulla retta e quindi, ricaviamo il generico centro :
![]()
e imponiamo che questo giacca su ![]()
![]()
![]()
![]()
![]()
Per determinare il luogo dei centri, studiamo il sistema:
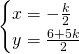
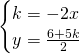
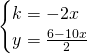
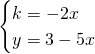 .
.
Ora, sapendo che il centro della circonferenza ha ascissa 2, avremo che:
![]()
![]()
da cui, ricaviamo la circonferenza:
![]()
![]()
![]()
e ricaviamo il raggio:
![]()
(Questa pagina è stata visualizzata da 90 persone)
