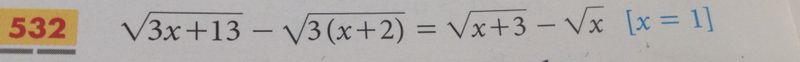Oggetto: disequazioni irrazionali
Corpo del messaggio:
Risposta dello staff
![]()
Studiamo le condizioni di esistenza:
![]()
![]()
![]()
![]()
Quindi la soluzione, nel caso esista, deve essere positiva.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Da cui, delle due soluzioni, solo una è accettabile, ovvero ![]()
(Questa pagina è stata visualizzata da 53 persone)