Oggetto: problema con triangolo

Corpo del messaggio:
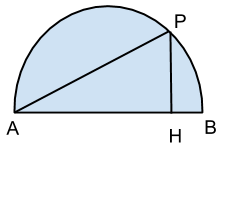
Considera una semicirconferenza di diametro AB=2r. Sia un punto P appartenente alla semicirconferenza e sia H la sua proiezione su AB.
Poni AH=x e determina x affinchè AH+PH sia >=  di 2r.

Risposta dello staff

Dalla traccia abbiamo che:

e, per il secondo teorema di Euclide, sapendo che un triangolo inscritto in una semicirconferenza è sempre rettangolo, avremo che:

Ciò che ci viene chiesto è:

Elevando al quadrato otteniamo:

da cui, essendo le due soluzioni e , otteniamo la soluzione della disequazione:

Escludiamo la possibilità di far coincidere il punto P con uno dei due estremi del diametro.

(Questa pagina è stata visualizzata da 66 persone)