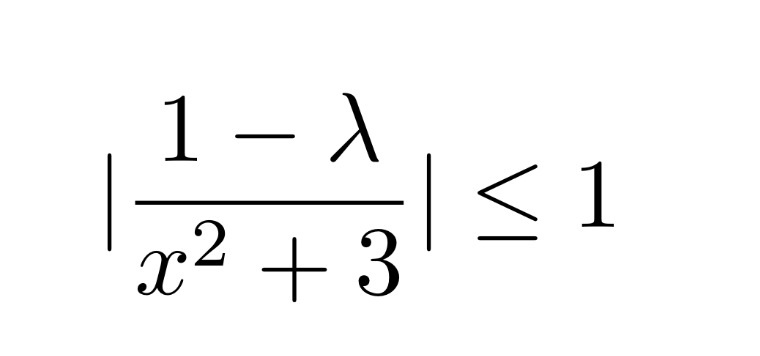Oggetto:
Corpo del messaggio:
Svolgere la seguente disequazione:
Risposta dello staff
Dato che ![]() è sempre positivo ci limiteremo a studiare:
è sempre positivo ci limiteremo a studiare:
![]()
![]()
Quindi, se ![]() , avremo:
, avremo:
![]()
![]()
![]()
Quindi:
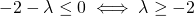 la disequazione è sempre verificata. Intersecando con la condizione iniziale avremo:
la disequazione è sempre verificata. Intersecando con la condizione iniziale avremo:
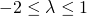 sempre verificata.
sempre verificata.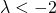 avremo che la soluzione della disequazione è:
avremo che la soluzione della disequazione è:
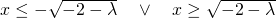
Analizziamo ora per ![]() .
.
![]()
![]()
Quindi, per ![]() la disequazione sarà sempre verificata.
la disequazione sarà sempre verificata.
per ![]() , l’equazione sarà verificata per:
, l’equazione sarà verificata per:
![]()
Unendo ora il tutto avremo:

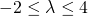 la disequazione è sempre verificata
la disequazione è sempre verificata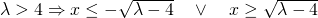
(Questa pagina è stata visualizzata da 51 persone)