Scrivere l’equazione della parabola con asse di simmetria parallelo all’asse delle ordinate, avente vertice nel punto V(5;-1) e che taglia l’asse y nel punto di ordinata 3.
Risposta dello staff
L’equazione sarà del tipo:
![]()
Passando per ![]() , avremo subito che:
, avremo subito che:
![]() .
.
Sapendo il vertice calcoliamo le altre due incognite:
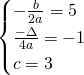
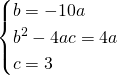
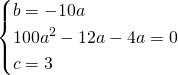
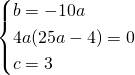
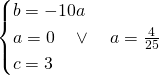
Escludendo la soluzione ![]() che renderebbe la parabola degenere, otteniamo:
che renderebbe la parabola degenere, otteniamo:
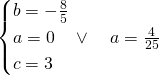
da cui:
![]()
(Questa pagina è stata visualizzata da 54 persone)