Gabriele scrive: Sistemi lineari

Pubblicato il da Lo StaffLascia un commento
0

Oggetto: Sistemi lineari

Es 198

Corpo del messaggio:

image (9)

 

 

Risposta dello staff

\begin{cases} \frac 12 (x-2y)(2x-y)-\frac 13 x(3x-1)=\frac 13 y\left(1-\frac {15}{2} x + 3y\right)+\frac 56 \\ \frac 12 (3x-1)-\frac 13 (y-2x)=\frac 32x+\frac 16 (2y+7) \end{cases}

\begin{cases} 3(x-2y)(2x-y)-2x(3x-1)=2y\left(1-\frac {15}{2} x + 3y\right)+ 5 \\ 3(3x-1)-2(y-2x)=9x+2y+7 \end{cases}

\begin{cases} 6x^2-3xy-12xy+6y^2-6x^2+2x=2y-15 xy + 6y^2+ 5 \\ 9x-3-2y+4x=9x+2y+7 \end{cases}

\begin{cases} 2x-2y= 5 \\ 4x-4y=10 \end{cases}

\begin{cases} 2x-2y= 5 \\ 2x-2y=5 \end{cases}

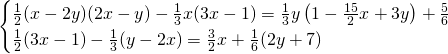
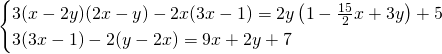
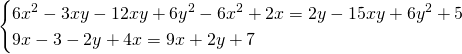
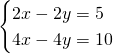
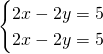
Senza bisogno di fare grossi calcoli, notiamo subito che abbiamo due equazioni identiche e quindi, non avremo mai un’unica soluzione. Il sistema è quindi indeterminato; basterà applicare il metodo di riduzione e sottrarre le due righe tra di loro per ottenere:

0x+0y=0

E quindi, per qualsiasi valore di x, esiste un valore di y che verifica ambedue le equazioni.

(Questa pagina è stata visualizzata da 54 persone)

Lascia un commento