Oggetto: esercizio 12 geometria analitica
Corpo del messaggio:
E’ l’esercizio 12 nella foto
Risposta dello staff
Date le due circonferenze:
![]()
e
![]()
a) affinchè siano concentriche deve verificarsi che, data certa l’esistenza, i due centri coincidano, quindi:
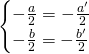
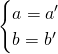
b) Visto che già prima abbiamo verificato come debbano avere lo stesso centro, a questa
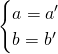
viene aggiunta la condizione di appartenenza alla bisettrice, ovvero alla retta di equazione:
![]()
da cui:
![]() .
.
c)
affinchè passi per l’origine, il termine noto deve essere nullo e quindi:
![]()
d)
Affinchè siano entrambe tangenti nello stesso punto all’asse x, deve verificarsi che:
![]()
e
![]()
da cui, a prescindere dalla x, avremo:
![]() ,
,
ed inoltre che il ![]()
da cui:
![]()
e quindi:
![]()
(Questa pagina è stata visualizzata da 103 persone)
