Michela scrive: problema su parabola

Pubblicato il da Lo StaffLascia un commento
0

Oggetto: problema su parabola

Corpo del messaggio:
Fra le parabole del tipo y= ax^2+bx+c:
a) determina la parabola p1 passante per A (-3; 4)e B (5; 8) e avente ascissa del vertice uguale a 2;
b) individua la parabola p2 passante per A e B e per il punto (1; 2);
c) conduci una  retta parallela all’asse y nella parte di piano delimitata da p1 e p2 in modo che, intersecando le due parabole, si formi un segmento lungo 2.

 

Risposta dello staff

a)

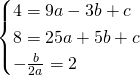
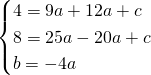
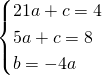
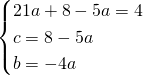
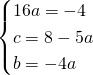
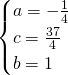
\begin{cases} 4=9a-3b+c \\ 8=25a+5b+c \\ -\frac{b}{2a}=2 \end{cases}

\begin{cases} 4=9a+12a+c \\ 8=25a-20a+c \\ b=-4a \end{cases}

\begin{cases} 21a+c=4 \\ 5a+c=8 \\ b=-4a \end{cases}

\begin{cases} 21a+8-5a=4 \\ c=8-5a \\ b=-4a \end{cases}

\begin{cases} 16a=-4 \\ c=8-5a \\ b=-4a \end{cases}

\begin{cases} a=-\frac 14 \\ c=\frac{37}{4} \\ b=1 \end{cases}

y=-\frac 14 x^2 +x+\frac{37}{4}

b)

\begin{cases} 4=9a-3b+c \\ 8=25a+5b+c \\ 2=a+b+c \end{cases}

\begin{cases} 9a-3b+2-a-b=4 \\ 25a+5b+2-a-b=8 \\ c=2-a-b \end{cases}

\begin{cases} 8a-4b=2 \\ 24a+4b=6 \\ c=2-a-b \end{cases}

\begin{cases} 4a-2b=1 \\ 12a+2b=3 \\ c=2-a-b \end{cases}

\begin{cases} 16a=4 \\ 2b=3-12a \\ c=2-a-b \end{cases}

\begin{cases} a=\frac 14 \\ b=0 \\ c=\frac 74 \end{cases}

y=\frac 14 x^2 + \frac 74

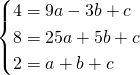
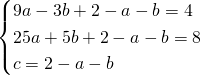
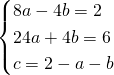
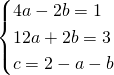
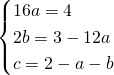
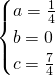
c)

Una generica retta parallela all’asse y è:

x=k

Quindi ci serve che la distanza delle ordinate tra le due parabole deve essere 2 e quindi:

|-\frac 14 x^2 +x+\frac{37}{4}-\frac 14 x^2 - \frac 74|=2

|-2 x^2 +4x+30|=8

|- x^2 +2x+15|=4

Risolviamo le due equazioni quindi:

- x^2 +2x+15=4 \quad \lor \quad - x^2 +2x+15=-4

x^2 -2x-11=0 \quad \lor \quad x^2 -2x-19=0

da cui:

x_{\frac 12}= \frac {2 \pm \sqrt{4+44}}{2}=\frac {2 \pm 4\sqrt{3}}{2}=1 \pm \sqrt 3

x_{\frac 34}= \frac {2 \pm \sqrt{4+76}}{2}=\frac {2 \pm 4\sqrt{5}}{2}=1 \pm \sqrt 5

(Questa pagina è stata visualizzata da 179 persone)

Lascia un commento