Valentina scrive: problema su circonferenza

Pubblicato il da Lo StaffLascia un commento
-2

Oggetto: problema su circonferenza

Corpo del messaggio:
Trova l’equazione della circonferenza y1, di centro (2; 1) e tangente alla retta di equazione 4x-3y=0, e l’equazione della circonferenza y2 passante per l’origine degli assi, per il punto (√3;1) e con un diametro che si trova sulla retta di equazione y=x+2. Considera poi il punto P (-1; 3) e, indicati con Q e R i punti di intersezione di y1 e y2, determina l’area del triangolo PQR.

Risposta dello staff

Sapendo che l’equazione della circonferenza generica di centro C(a,b) è:

x^2+y^2-2ax-2by+c=0

la circonferenza y_1 sarà del tipo:

x^2+y^2-4x-2y+c=0

Per ricavare c, imponiamo che, studiando l’intersezione con la retta y=\frac 43 x, il \Delta sia uguale a 0:

x^2+\frac{16}{9}x^2-4x-\frac 83x+c=0

25x^2-60x+9c=0

Studiamo il \Delta e otteniamo:

\Delta=3600-900c

Imponendo l’uguaglianza a 0 avremo:

c=4

La prima circonferenza quindi avrà equazione:

x^2+y^2-4x-2y+4=0

Troviamo la seconda equazione, sapendo che passa per l’origine sarà:

x^2+y^2-2ax-2by=0

Le altre due condizioni ci dicono che:

\begin{cases} 3+1-2\sqrt 3 a -2b=0\\ b=a+2 \end{cases}

\begin{cases} \sqrt 3 a +b=2\\ b=a+2 \end{cases}

\begin{cases} \sqrt 3 a +a+2=2\\ b=a+2 \end{cases}

\begin{cases} a=0\\ b=2 \end{cases}

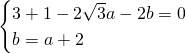
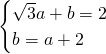
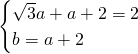
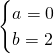
da cui:

x^2+y^2-4y=0

Ricaviamo i punti di intersezione tra le due circonferenza:

\begin{cases}x^2+y^2-4x-2y+4=x^2+y^2-4y \\ x^2+y^2-4y=0 \end{cases}

\begin{cases} -4x+2y+4=0 \\ x^2+y^2-4y=0 \end{cases}

\begin{cases} 2x-y-2=0 \\ x^2+y^2-4y=0 \end{cases}

\begin{cases} y=2x-2 \\ x^2+(2x-2)^2-4(2x-2)=0 \end{cases}

\begin{cases} y=2x-2 \\ x^2+4x^2-8x+4-8x+8=0 \end{cases}

\begin{cases} y=2x-2 \\ 5x^2-16x+12=0 \end{cases}

\begin{cases} y=2x-2 \\ x_{\frac 12}=\frac{16 \pm \sqrt{256-240}}{10}\end{cases}

\begin{cases} y=2x-2 \\ x_{\frac 12}=\frac{16 \pm 4}{10}\end{cases}

\begin{cases} y=2x-2 \\ x_1=\frac{6}{5} \quad \wedge \quad x_2=2\end{cases}

\begin{cases} y_1=\frac 25 \quad \wedge \quad y_2=2\\ x_1=\frac{6}{5} \quad \wedge \quad x_2=2\end{cases}

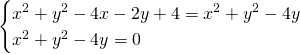
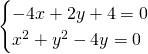
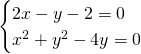
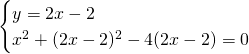
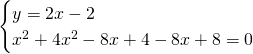
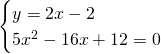
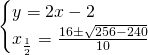
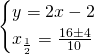
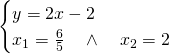
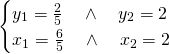
Ora abbiamo i tre punti:

P(-1;3)

Q(\frac 65; \frac 25)

R(2;2)

Sapendo i 3 punti la formula per calcolare l’area è:

A=\left| (x_R-x_P)(y_Q-y_P)-(x_Q-x_P)(y_R-y_P) \right|

Sostituiamo e otteniamo:

A=\left| (2+1)(\frac 25 - 3)-(\frac 65+1)(2-3) \right|=\left|-\frac{39}{5}-\frac 65 \right|=15

 

(Questa pagina è stata visualizzata da 181 persone)

Lascia un commento