Francesco scrive: l’equazione della circonferenza

Pubblicato il da Lo Staff2 commenti
-6

Oggetto: l’equazione della circonferenza

Corpo del messaggio:
1)scrivi il luogo geometrico dei punti del piano che hanno distanza   radq 5 dal punto (-3,1)

Risposta dello staff

(x+3)^2+(y-1)^2=5
2)determina l’equazione della circonferenza avente centro C(2,-3) e raggio di lunghezza uguale a quella del segmento di estremi (-2;2/3) e (1,-5/2)

r= \sqrt{(-2-1)^2+ (\frac 23 + \frac 52)^2}=\sqrt{9+\frac{361}{36}}=\sqrt{\frac{685}{36}}

C: (x-2)^2+ (y+3)^2=\frac{685}{36}
3)scrivi l’equazione della circonferenza di centro C(0,3)e per passante per P(2,-1)

x^2+(y-3)^2=r^2

4+16=r^2

r^2=20

C: x^2+(y-3)^2=20
4)determina l’equazione della circonferenza di centro C(-1,1)e passante per A(0,-2)

(x+1)^2+(y-1)^2=r^2

1+9=r^2

r^2=10

C: (x+1)^2+(y-1)^2=10
5)scrivi l’equazione della circonferenza di raggio 3 il cui centro sia il punto p(4/3,-1/2

(x-\frac 43)^2 + (y+\frac 12)^2=9
6) trova l’equazione della circonferenza di raggio 2 radq3 avente il centro nel punto in cui la retta di equazione 2x+3y=5 interseca la bisettrice del I quadrante

Troviamo il centro:

\begin{cases} x=y \\ 2x+3y=5 \end{cases}

\begin{cases} x=y \\ 5y=5 \end{cases}

\begin{cases} x=1 \\ y=1 \end{cases}

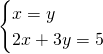
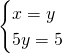
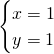
Quindi la circonferenza sarà.

(x-1)^2+(y-1)^2=12

(Questa pagina è stata visualizzata da 113 persone)

2 pensieri riguardo “Francesco scrive: l’equazione della circonferenza”

Lascia un commento