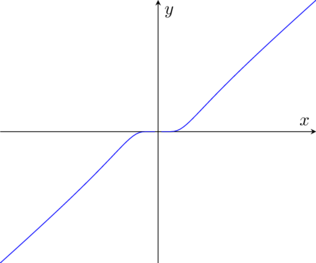
Studiare l’andamento della funzione:
![Rendered by QuickLaTeX.com \[f(x)=\begin{cases} x e^{-\frac{1}{x^2}} \qquad x \neq 0 \\ 0 \qquad x =0\]](https://www.matebook.it/wp-content/ql-cache/quicklatex.com-62d6e8407a825a2d711d896a7353b4ab_l3.png)
Risposta dello staff
Per costruzione, il dominio sarà tutto ![]() .
.
Visto che la funzione esponenziale è sempre positiva, la positività dipende dalla x, e quindi:
![]()
![]()
![]()
Studiamo parità e disparità:
![]()
![]()
La funzione è quindi dispari.
Studiamo i limiti all’infinito:
![]()
Studiamo la derivata prima:
![]()
![]()
![]()
Essendo due fattori entrambi strettamente positivi avremo:
![]()
![]()
Studiamo la derivata seconda:
![]()
![]()
Di conseguenza avremo che:
![]()
![]()
(Questa pagina è stata visualizzata da 47 persone)