Claudio scrive: Problemi con la parabola 244

Pubblicato il da EdoLascia un commento
-1

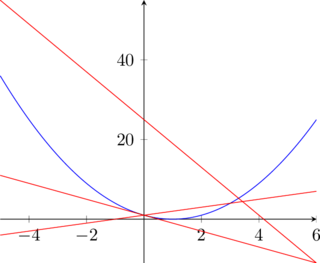
Considera la parabola avente equazione y=x^2-2x+1 e tracciane il grafico. Indica con A e B (x_A<x_B) i punti in cui la retta di equazione y=x+1 interseca la parabola e determina il punto P dell’arco AB di parabola in corrispondenza del quale è massima l’area del triangolo APB.

P 3/2 1/4

Risposta dello staff

Troviamo i due punti di intersezione:

\begin{cases} y=x^2-2x+1 \\ y=x+1\end{cases}

\begin{cases} x+1=x^2-2x+1 \\ y=x+1\end{cases}

\begin{cases} x^2-3x=0 \\ y=x+1\end{cases}

\begin{cases} x_1=0 \quad x_2=3 \\ y=x+1\end{cases}

\begin{cases} x_1=0 \quad x_2=3 \\ y_1=1 \quad y_2=4\end{cases}

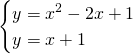
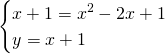
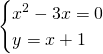
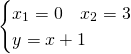
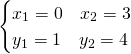
Per calcolare l’area usiamo la regola di Sarrus, sapendo che il generico punto P avrà coordinate (x;x^2-2x+1)

\begin{vmatrix} x & y \\ z & v \end{vmatrix}

A=\frac 12 \begin{vmatrix} 0 & 1 & 1 \\ 3 & 4 & 1 \\ x & x^2-2x+1 & 1\end{vmatrix}

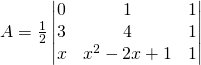
da cui:

A=\left|\frac 12(x+3(x^2-2x+1)-4x-3) \right|=\left|\frac 12 (x+3x^2-6x+3-4x-3)\right|=\left|\frac32x (x-3)\right|

L’area massima

Rendered by QuickLaTeX.com

(Questa pagina è stata visualizzata da 71 persone)

Lascia un commento