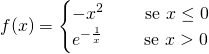
Risposta dello staff
Dominio
Essendo una funzione a tratti formata da una funzione polinomiale e da una funzione esponenziale, dove però, in essa, viene escluso lo 0, valore che annulla il denominatore, il dominio di f sarà tutto ![]()
Positività
Si nota subito che la funzione sarà positiva per ![]() , per definizione di esponenziale, sarà negativa per
, per definizione di esponenziale, sarà negativa per ![]() , poichè
, poichè ![]() per
per ![]() , e sarà nulla per
, e sarà nulla per ![]() .
.
![]()
![]()
![]()
L’unica intersezione con gli assi sarà l’origine, e la funzione in 0 risulta continua.
![]()
![]()
Studiamo i limiti agli estremi:
![]()
![]()
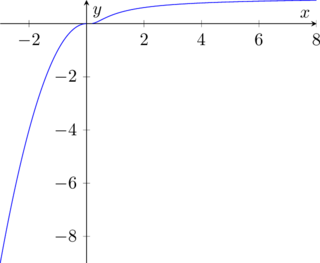
Questa funzione avrà asintoto orizzontale destro in ![]() , ma non lo avrà a sinistra in quanto la funzione nella parte sinistra del grafico è una parabola.
, ma non lo avrà a sinistra in quanto la funzione nella parte sinistra del grafico è una parabola.
Studiamo la derivata prima:
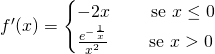
La funzione non ammetterà ne massimi ne minimi relativi; in 0 la funzione non sarà derivabile perchè i limiti della derivata prima calcolati in 0 sono diversi.
![]()
![]()
Avremo quindi:
![]()
Studiamo la derivata seconda:
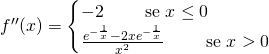
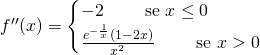
Quindi, per ![]() la funzione è concava,
la funzione è concava,
Per ![]() la funzione sarà convessa per
la funzione sarà convessa per ![]() , concava per
, concava per ![]() e ammetterà in
e ammetterà in ![]() un punto di flesso.
un punto di flesso.
(Questa pagina è stata visualizzata da 74 persone)