Pasquale scrive: Problema con equazioni I grado

Pubblicato il da Lo StaffLascia un commento
0

Oggetto: Problema con equazioni I grado

Corpo del messaggio:
In una circonferenza il diametro AB, di lunghezza 40 cm, è diviso da un punto H in due parti tali che 5 AH + HB = 9/5 AB.
Detta CD la corda cui appartiene H, perpendicolare ad AB, calcola l’area del quadrilatero ABCD.

circonferenza con corda

Risposta dello staff

Troviamo subito la lunghezza dei due segmenti. Chiamando con  x e y i due segmenti otteniamo:

\begin{cases} x+y=40 \\ 5x+y=\frac 95 40\end{cases}

\begin{cases} x+y=40 \\ 5x+y=72\end{cases}

\begin{cases} x+y=40 \\ 4x=32\end{cases}

\begin{cases} y=32 \\ x=8\end{cases}

AH=8 \mbox{ cm}

BH=32 \mbox{ cm}

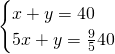
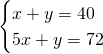
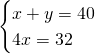
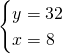
Visto che, tracciando la perpendicolare, si verranno a creare due triangoli rettangoli uguali. Per calcolare l’area del quadrilatero, basterà raddoppiare l’area di un triangolo, quindi, ricaviamo l’altezza con il teorema di Talete:

CH=\sqrt{AH \cdot HB}=\sqrt{8 \cdot 32} \mbox{ cm}=16\mbox{ cm}

L’area del quadrilatero sarà quindi:

A=2\cdot \frac{AB \cdot CH}{2}=(40 \cdot 16)\mbox{ cm}^2=640 \mbox{ cm}^2

(Questa pagina è stata visualizzata da 57 persone)

Lascia un commento