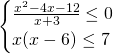
Risposta dello staff
Discutiamo separatamente le due disequazioni.
![]()
Studiamo il numeratore:
![]()
![]()
Le due soluzioni dell’equazione associata sono:
![]()
![]()
per cui la soluzione della disequazione è:
![]()
Studiamo il denominatore:
![]()
Mettendo insieme le soluzioni e prendendo solo le negative otteniamo:
![]()
Risolviamo la seconda disequazione del sistema:
![]()
![]()
![]()
Le due soluzioni dell’equazione associata sono:
![]()
![]()
per cui la soluzione della disequazione è:
![]()
Il sistema diventerà quindi:
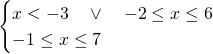
Mettendo a sistema le soluzioni otteniamo la soluzione:
![]()
(Questa pagina è stata visualizzata da 34 persone)