Oggetto: equazione iperbole
Corpo del messaggio:
determina l’equazione dell’iperbole con i fuochi sull’asse delle x avente un asintoto di equaione 3x+4y=0 e passante per ![]() .
.
Risposta dello staff
L’equazione dell’iperbole avente i fuochi sull’asse x è:
![]()
Riscrivendo l’equazione dell’asintoto ricaviamo una relazione tra a e b:
![]()
Ora, mettendo a sistema questa con il passaggio per il punto, ricaviamo le due incognite:
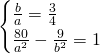
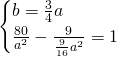
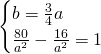
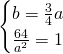
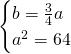
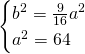
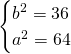
Per cui l’equazione sarà:
![]()
(Questa pagina è stata visualizzata da 64 persone)