Oggetto: studio di funzione
Corpo del messaggio:
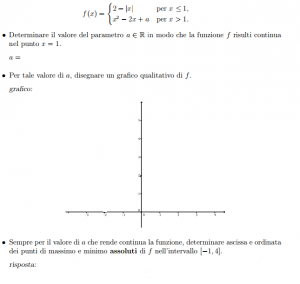
Salve, vi allego la foto perchè è molto più semplice da vedere, non riesco a risolvere questo tipo di esercizio, anche una risposta teoria sul procedimento potrebbe essere d’aiuto. Vi ringrazio anticipatamente
Risposta dello staff
Riscrivendola meglio avremo:
Ora, affinchè sia continua in 1 deve verificarsi che:
sia uguale a
Per cui:
Dal grafico si nota subito che ci sono due minimi assoluti, ovvero
Il massimo si avrà in corrispondenza di 4:
(Questa pagina è stata visualizzata da 102 persone)