Ilaria scrive: Aiuto problemi con aree

Pubblicato il da Lo StaffLascia un commento
-1

Oggetto: Aiuto problemi con aree.

Corpo del messaggio:
Salve ci sono due problemi  che non ho capito.
1. L’area di un quadrato è 400cm2. Calcola l’area di un rettangolo avente il perimetro congruente a 5/4 di quello del quadrato, sapendo che l’altezza é 2/3 della base.
2.Un rombo è equivalente a un quadrato il cui perimetro è 120cm.Calcola il perimetro del rombo sapendo che la sua altezza misura18cm.
3.Un triangolo ha la base che misura 27cm e l’altezza è 8/9 della base. Calcola il perimetro e l’area di un quadrato equivalente al triangolo.

Risposta dello staff

1)

Sapendo l’area del quadrato, calcoliamo il suo lato:

l_Q=\sqrt{400} \mbox{ cm}=20\mbox{ cm}

2p_Q=80\mbox{ cm}

Ricaviamo ora il perimetro del rettangolo:

2p_R=\frac 54 80\mbox{ cm}=100\mbox{ cm}

Ora, sapendo la relazione tra base e altezza avremo:

\begin{cases} h=\frac 23 b \\ 2h+2b=100\end{cases}

\begin{cases} h=\frac 23 b \\ \frac 43b+2b=100\end{cases}

\begin{cases} h=\frac 23 b \\ \frac {10}{3}b=100\end{cases}

\begin{cases} h=20 \mbox{ cm} \\ b=30 \mbox{ cm}\end{cases}

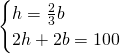
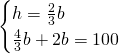
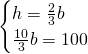
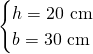
L’area sarà:

A=b\cdot h=600\mbox{ cm}^2

2)

Ricaviamo il lato del quadrato:

l_Q=30 \mbox{ cm}

l’area, uguale per ambedue i poligoni, sarà quindi:

A_Q=900 \mbox{ cm}^2

Il lato del rombo lo ricaviamo come rapporto tra l’area e altezza e quindi:

l_R=\frac{900}{18}\mbox{ cm}=50\mbox{ cm}

Il perimetro del rombo sarà quindi:

2p=200 \mbox{ cm}

3)

L’altezza del triangolo sarà:

h=\frac 89 27\mbox{ cm}=24 \mbox{ cm}

L’area del triangolo, e quindi del quadrato, sarà:

A=\frac{24 \cdot 27}{2}=\mbox{ cm}^2=324\mbox{ cm}^2

Il lato del quadrato sarà:

l_Q=\sqrt{324}\mbox{ cm}=18\mbox{ cm}

Il perimetro:

2p=72\mbox{ cm}

(Questa pagina è stata visualizzata da 69 persone)

Lascia un commento