Mattia scrive: esercizio sul valore assoluto

Pubblicato il da Lo StaffLascia un commento
0

Oggetto: esercizio sul valore assoluto

Corpo del messaggio:
|x-1|+ |x(allaseconda)+5x-6|>0

Risposta dello staff

|x-1| + |x^2+5x-6|>0

Essendo la somma di due valori assoluti, questa sarà sempre strettamente positiva a meno di trovare un valore che annulli entrambi.

Studiamo separatamente i valori assoluti:

x-1 \geq 0 \iff x \geq 1

x^2+5x-6 \geq 0 \iff x \leq -6 \quad \lor \quad x \geq 1

Avremo quindi che la disequazione è verificata sempre tranne che per x=1

Studiamo anche in un altro modo, svolgendo i tre sistemi separatamente:

\begin{cases} x \leq -6 \\ 1-x+x^2+5x-6>0 \end{cases} \quad \quad\begin{cases} -6 <x <1 \\ 1-x-x^2-5x+6>0 \end{cases} \quad \quad\begin{cases} x \geq 1 \\ x-1+x^2+5x-6>0 \end{cases}

\begin{cases} x \leq -6 \\ x^2+4x-7>0 \end{cases} \quad \quad\begin{cases} -6 <x <1 \\ -x^2-6x+7>0 \end{cases} \quad \quad\begin{cases} x \geq 1 \\ x^2+6x-7>0 \end{cases}

\begin{cases} x \leq -6 \\ x< -2-\sqrt {11} \quad \lor \quad x> -2+\sqrt {11} \end{cases} \quad \quad\begin{cases} -6 <x <1 \\ -7<x<1 \end{cases} \quad \quad\begin{cases} x \geq 1 \\ x<-7 \quad \lor \quad x>1 \end{cases}

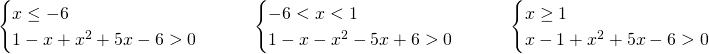
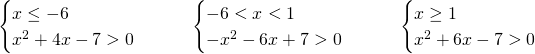
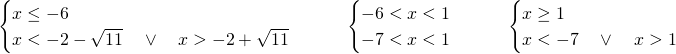
Unendo tutto avremo che è sempre verificata in ogni intervallo e quindi ammette sempre soluzione come detto ad inizio esercizio escludendo solo x=1, che renderebbe nulla la somma.

(Questa pagina è stata visualizzata da 32 persone)

Lascia un commento