Solange scrive: Verifica

Pubblicato il da Lo StaffLascia un commento
0

Oggetto: Verifica

Corpo del messaggio:
Non so come fare questi esercizi
Aiutatemi vi prego

img-20151214-wa0018-765x1024

Risposta dello staff

4)

La risposta esatta è la D, in quanto, in un sistema di disequazioni, va fatta l’intersezione delle soluzioni.

5)

La risposta esatta è la D per definizione di valore assoluto.

6)

La risposta esatta è la A. -2 non è soluzione poichè avremmo 0=-16.

7)

La risposta esatta è la C, in quanto andrebbero studiare due disequazioni differenti e poi unire le soluzioni:

\begin{cases} x < -\sqrt 7 \quad \lor \quad x > \sqrt 7 \\ x^2-7>2\end{cases} \quad \quad \quad \begin{cases} -\sqrt 7\leq x \leq \sqrt 7 \\ -x^2+7>2\end{cases}

\begin{cases} x < -\sqrt 7 \quad \lor \quad x > \sqrt 7 \\ x^2>9\end{cases} \quad \quad \quad \begin{cases} -\sqrt 7\leq x \leq \sqrt 7 \\ x^2<5\end{cases}

\begin{cases} x < -\sqrt 7 \quad \lor \quad x > \sqrt 7 \\ x<-3 \quad \lor \quad x>3 \end{cases} \quad \quad \quad \begin{cases} -\sqrt 7\leq x \leq \sqrt 7 \\ -\sqrt 5<x< \sqrt 5\end{cases}

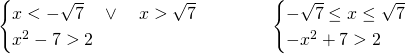
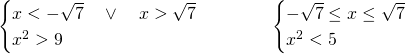
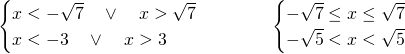
8)

La risposta esatta è la C, in quanto andrebbero studiare due disequazioni differenti e poi unire le soluzioni:

\begin{cases} x < -\sqrt {10} \quad \lor \quad x > \sqrt {10} \\ x^2-10<1 \end{cases} \quad \quad \quad \begin{cases} -\sqrt {10}\leq x \leq \sqrt {10} \\ -x^2+10<1\end{cases}

\begin{cases} x < -\sqrt {10} \quad \lor \quad x > \sqrt {10} \\ x^2<11 \end{cases} \quad \quad \quad \begin{cases} -\sqrt {10}\leq x \leq \sqrt {10} \\ x^2>9\end{cases}

\begin{cases} x < -\sqrt {10} \quad \lor \quad x > \sqrt {10} \\ -\sqrt{11}<x<\sqrt{11} \end{cases} \quad \quad \quad \begin{cases} -\sqrt {10}\leq x \leq \sqrt {10} \\ x<-3 \quad \lor \quad x>3\end{cases}

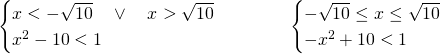
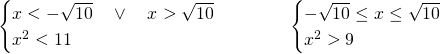
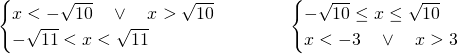
(Questa pagina è stata visualizzata da 30 persone)

Lascia un commento