- La distanza tra due punti
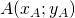 e
e 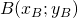 è data dalla relazione
è data dalla relazione
![]() .
.
Nel caso in cui i due punti abbiano la stessa ascissa o la stessa ordinata la loro distanza è data da:
![]() se
se![]() ;
;
![]() se
se![]() .
.
- Il punto medio
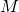 di un segmento
di un segmento 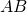 di estremi
di estremi 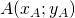 e
e 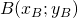 ha coordinate:
ha coordinate:
![]() .
.
- L’equazione di una retta si può presentare in:
- forma implicita
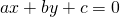 con
con 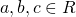 .
. - forma esplicita
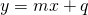 con
con 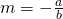 ,
, 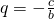 e
e 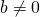 ,
,
dove ![]() è il coefficiente angolare e
è il coefficiente angolare e ![]() il termine noto o ordinata all’origine.
il termine noto o ordinata all’origine.
Tra le rette particolari ricordiamo:
- asse
 :
: 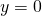 ; asse
; asse 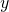 :
: 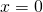 ;
; - parallela all’asse
 :
: 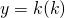 ; parallela all’asse
; parallela all’asse 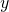 :
: 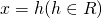 ;
; - bisettrice I-III quadrante
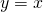 ; bisettrice II-IV quadrante
; bisettrice II-IV quadrante 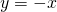 .
.
- La retta di coefficiente angolare
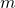 e passante per il punto
e passante per il punto 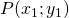 ha equazione:
ha equazione:
![]() .
.
In particolare, la retta passante per l’origine ![]() è:
è:
![]() .
.
L’insieme di rette ![]() prende anche il nome di fascio di rette di centro o sostegno
prende anche il nome di fascio di rette di centro o sostegno ![]() .
.
- La retta passante per i punti
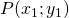 e
e 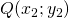 con
con 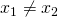 e
e 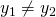 , ha equazione
, ha equazione
![]() o anche
o anche ![]()
con
![]() .
.
Nel caso in cui i due punti abbiano la stessa ascissa ![]() o la stessa ordinata
o la stessa ordinata ![]() , la retta da essi individuata ha equazione:
, la retta da essi individuata ha equazione:
![]() oppure
oppure ![]() .
.
- Due rette
 ed
ed  , non parallele all’asse
, non parallele all’asse 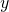 , e rispettivamente di coefficiente angolare
, e rispettivamente di coefficiente angolare 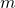 e
e 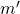 sono tra loro:
sono tra loro:
- parallele se e solo se

- perpendicolari se e solo se
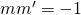 o
o 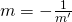 .
.
- La distanza del punto
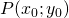 dalla retta
dalla retta  di equazione
di equazione ![Rendered by QuickLaTeX.com ax+by+c=0 [y=mx+q]](https://www.matebook.it/wp-content/ql-cache/quicklatex.com-8a65e42f72d9aa1298f78fdcfd06d306_l3.png) è data dalle formule:
è data dalle formule:
![]() [
[![]() .
.
Se i punti ![]() ,
, ![]() e
e ![]() non sono allineati (per verificarlo basta determinare l’equazione della retta passante per due di essi e constatare che il terzo punto non le appartiene, cioè le sue coordinate non soddisfano l’equazione), l’area del triangolo
non sono allineati (per verificarlo basta determinare l’equazione della retta passante per due di essi e constatare che il terzo punto non le appartiene, cioè le sue coordinate non soddisfano l’equazione), l’area del triangolo ![]() è data dal seguente valore assoluto del determinante
è data dal seguente valore assoluto del determinante
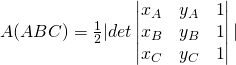 .
.
Altri hanno visualizzato anche
- Circonferenza
- Ellisse
- Iperbole
- Parabola
- Punto retta
- Retta
- Rette tangenti ad una conica
- Trasformazioni geometriche piane
- Triangoli
(Questa pagina è stata visualizzata da 287 persone)