- Traslazione
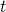 degli assi
degli assi
Gli assi ![]() e
e ![]() sono paralleli ed equiversi, rispettivamente, all’asse
sono paralleli ed equiversi, rispettivamente, all’asse ![]() e all’asse
e all’asse ![]() . Il punto
. Il punto ![]() è l’origine degli assi
è l’origine degli assi ![]() e
e ![]() .
.
- Rotazione degli assi
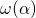 di centro
di centro 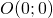 e angolo orientato
e angolo orientato 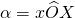
![]()
- Rototraslazione degli assi
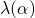
Gli assi di riferimento ![]() e
e ![]() sono paralleli ed equiversi, rispettivamente, all’asse
sono paralleli ed equiversi, rispettivamente, all’asse ![]() e all’asse
e all’asse ![]() . Il punto
. Il punto ![]() è l’origine degli assi
è l’origine degli assi ![]() e
e ![]() e degli assi
e degli assi ![]() e
e ![]() . L’angolo orientato di rotazione è
. L’angolo orientato di rotazione è ![]() .
.
![]()
Altri hanno visualizzato anche:
- Affinità
- Dilatazioni
- Isometrie
- Omotetie
- Similitudini
- Trasformazioni relative al sistema di riferimento
(Questa pagina è stata visualizzata da 455 persone)