Si definisce omotetia di centro ![]() e di rapporto
e di rapporto ![]() , con
, con ![]() , ogni trasformazione geometrica piana che a ciascun punto
, ogni trasformazione geometrica piana che a ciascun punto ![]() del piano fa corrispondere il punto
del piano fa corrispondere il punto ![]() in modo che i punti
in modo che i punti ![]() ,
, ![]() siano allineati con
siano allineati con ![]() , dalla stessa parte se
, dalla stessa parte se ![]() , da parti opposte se
, da parti opposte se ![]() , e risulti
, e risulti ![]() .
.
Se ![]() l’omotetia coincide con la trasformazione identica, mentre se
l’omotetia coincide con la trasformazione identica, mentre se ![]() coincide con la simmetria centrale di centro
coincide con la simmetria centrale di centro ![]() .
.
- Omotetia di centro
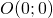 e rapporto
e rapporto 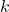 , con
, con 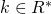
Ogni omotetia di centro 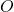 e rapporto
e rapporto 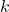 trasforma un angolo in un angolo a esso congruente, una retta in una retta a essa parallela, conserva l’allineamento, il parallelismo, l’incidenza e la perpendicolarità. In ogni omotetia di rapporto
trasforma un angolo in un angolo a esso congruente, una retta in una retta a essa parallela, conserva l’allineamento, il parallelismo, l’incidenza e la perpendicolarità. In ogni omotetia di rapporto 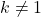 il centro è l’unico punto unito e le rette del fascio proprio con sostegno il centro
il centro è l’unico punto unito e le rette del fascio proprio con sostegno il centro 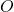 sono le uniche rette unite ma non fisse. Le omotetie sono dirette se
sono le uniche rette unite ma non fisse. Le omotetie sono dirette se 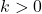 , invertenti se
, invertenti se 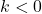 ; si definiscono ingrandimenti se
; si definiscono ingrandimenti se 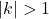 , riduzioni se
, riduzioni se 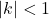 .
.
Se il centro di omotetia è un genetico punto ![]() si ha:
si ha:
![]() .
.
Altri hanno visualizzato anche:
- Affinità
- Dilatazioni
- Isometrie
- Omotetie
- Similitudini
- Trasformazioni relative al sistema di riferimento
(Questa pagina è stata visualizzata da 506 persone)