Traccia
![]()
Svolgimento
Per risolvere questa equazione possiamo utilizzare il metodo di:
- moltiplicare
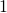 per
per 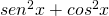 di modo che risulti una moltiplicazione per
di modo che risulti una moltiplicazione per 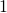 ;
; - dividere tutto per
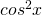 in modo da avere un’equazione in funzione della sola
in modo da avere un’equazione in funzione della sola 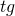 .
.
![]()
Imponendo che ![]() , otteniamo:
, otteniamo:
![]()
![]()
![]()
![]()
![]()
da cui avremo come soluzione:
![]()
![]()
Altri esercizi simili:
- Esercizio 1 Equazioni omogenee di secondo grado in seno e coseno
- Esercizio 2 Equazioni omogenee di secondo grado in seno e coseno
- Esercizio 3 Equazioni omogenee di secondo grado in seno e coseno
- Esercizio 4 Equazioni omogenee di secondo grado in seno e coseno
- Esercizio 5 Equazioni omogenee di secondo grado in seno e coseno
- Esercizio 6 Equazioni omogenee di secondo grado in seno e coseno
- Esercizio 7 Equazioni omogenee di secondo grado in seno e coseno
- Esercizio 8 Equazioni omogenee di secondo grado in seno e coseno
- Esercizio 9 Equazioni omogenee di secondo grado in seno e coseno
- Esercizio 10 Equazioni omogenee di secondo grado in seno e coseno
- Esercizio 11 Equazioni omogenee di secondo grado in seno e coseno
- Esercizio 12 Equazioni omogenee di secondo grado in seno e coseno
- Esercizio 13 Equazioni omogenee di secondo grado in seno e coseno
- Esercizio 14 Equazioni omogenee di secondo grado in seno e coseno
- Esercizio 15 Equazioni omogenee di secondo grado in seno e coseno
(Questa pagina è stata visualizzata da 215 persone)
Salve, non ho capito gli ultimi passaggi della risoluzione, in cui appare tgx=0 e tgx=rad3
Potreste spiegarmi il motivo di questo svolgimento?
C’era un errore di battitura nel mezzo… Riveduto e corretto.
E’ semplicemente svolto con la legge di annullamento del prodotto.