Esercizio 3 Problema di geometria piana risolubili con l’uso della trigonometria

-1

Traccia

In un triangolo isoscele inscritto in una circonferenza di raggio r, la somma del doppio dell’altezza con il triplo del lato è 4r. Determinare l’ampiezza dell’angolo al vertice.

 

 

Svolgimento

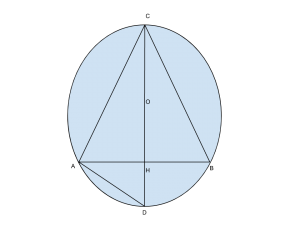
triangolo isoscele inscritto

 

Per comodità, imponiano che sia ABC un triangolo isoscele di base AB; per costruzione sappiamo che l’altezza relativa alla base divide essa stessa in due parti uguali ed, essendo il triangolo inscritto in una circonferenza allora è chiaro che l’altezza CH deve giacere lungo un diametro

Indicando con D l’intersezione tra il prolungamento dell’altezza e la circonferenza è facile osservare che il triangolo ACD è retto in  A dato che la corda sottesa dall’angolo alla circonferenza A coincide con il diametro ( o meglio, ACD è inscritto in una semicirconferenza).

Sia \alpha l’angolo alla base del triangolo isoscele ABC, per il teorema della corda si ha che

    \[AC = l = 2 r sen(\alpha)\]

Occorre esprimere l’altezza CH = h in termini del lato l e del raggio r

Si osserva che

    \[CH = CD - HD = 2 r - HD\]

,  dunque occorre ricavare HD.

Calcolo dapprima AD applicando il teorema di Pitagora al triangolo ACD

    \[(AD)^2 = (CD)^2 - (AC)^2 = 4 r^2 -l^2\]

poi applico il teorema di Talete al triangolo rettangolo ACD

    \[(AD)^2 = CD \cdot HD = 2 r HD\]

da cui

    \[HD =\frac {AD^2 }{ 2r} =\frac {4 * r^2 - l^2}{2r}\]

.

 

Possiamo quindi ricavare:

CH=2r- \frac {4r^2-l^2}{2r}=\frac {4r^2-4r^2+l^2}{2r}=\frac {l^2}{2r}=\frac {4r^2sen^2(\alpha)}{2r}=2rsen^2(\alpha)

Dalla traccia sappiamo che:

2CH+3AC=4r

e quindi:

2(2rsen^2(\alpha) + 3 (2rsen(\alpha))-4r=0

4rsen^2(\alpha)+6rsen(\alpha)-4r=0

Dividiamo tutto per 2r e otteniamo:

2sen^2(\alpha)+3sen(\alpha)-2=0

sen(\alpha)_{\frac 12}=\frac {-3 \pm \sqrt {9+16}}{4}=\frac {-3 \pm 5}{4}

Ovviamente non consideriamo la soluzione negativa perchè la funzione seno può assumere solo valori compresi tra -1 e 1.

Quindi accettiamo come soluzione solo:

sen(\alpha)=\frac 12

da cui, non consideriamo la soluzione 150^\circ perchè imporrebbe che la somma degli angoli interni sia maggiore di 180^\circ.

Unica soluzione accettabile sarà infine.

\alpha= 30^\circ

Ora, sapendo l’angolo alla base del triangolo, ricaviamo finalmente l’angolo al vertice:

\widehat{ACB}=180^\circ-2\cdot 30^\circ=120^\circ

 

 

 

 

Altri esercizi simili

(Questa pagina è stata visualizzata da 707 persone)

Lascia un commento