Soluzione e svolgimento dei seguenti problemi di geometria piana.

 

1. Il rapporto fra le dimensioni di un rettangolo è 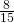e l’area è 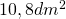. Trovare il perimetro.
2. L’area di un rombo è 960 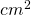, una diagonale è 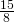dell’altra, trovare il perimetro del rombo.
3. Trovare l’altezza di un triangolo di base 12 cm tale che la sua area sia equivalente a quella di un quadrato il cui lato è 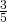dell’altezza del triangolo.
4. Il perimetro di un rombo è cm 204 e una diagonale è i 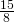dell’altra. Calcolare l’area del rombo.
5. Un rettangolo ha il perimetro di 80 cm e la base di 26 cm. Determinare i lati di un secondo rettangolo interno al data, con i lati equidistanti dai lati del primo e di area
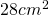
6. In un rettangolo la base supera di 24 cm i 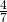dell’altezza. Determinare il perimetro del rettangolo sapendo che l’area è di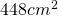
7. I lati di due quadrati differiscono di a, la somma delle loro aree è 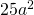; trovare i lati dei due quadrati
8. I lati di un rettangolo sono lunghi 20 cm e 30 cm. Aumentando i lati di due segmenti di eguale lunghezza, l’area aumenta di 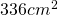. Calcolare le lunghezze di tali segmenti.
9. Dato il quadrato ABCD di lato l, determinare sulla retta AB un punto P tale che la somma dei quadrati delle sue distanze dai vertici C e D sia
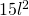
10. In un triangolo isoscele la base supera di a l’altezza, mentre ciascuno dei due lati congruenti supera di a la base. Trovare il perimetro e l’area del triangolo.
11. Determinare le lunghezze dei lati di un trapezio rettangolo, di area 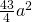, sapendo che la diagonale minore è lunga 5a e che l’altezza supera di a la base minore.
12. In un triangolo rettangolo un cateto è lungo cm 45 e la sua proiezione sull’ipotenusa è i 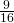della proiezione dell’altro cateto sull’ipotenusa. Trovare perimetro ed area del triangolo.

(Questa pagina è stata visualizzata da 721 persone)