Traccia
Determinare i valori del parametro ![]() per cui l’equazione
per cui l’equazione ![]() ha due soluzioni distinte, entrambe negative.
ha due soluzioni distinte, entrambe negative.
Svolgimento
![]()
![]()
Per capire per quali valori di ![]() l’equazione avrà sempre soluzioni reali, basterà semplicemente studiare la positività del
l’equazione avrà sempre soluzioni reali, basterà semplicemente studiare la positività del ![]() .
.
![]()
![]()
![]()
![]()
![]()
Imponiamo ora che ![]() e avremo:
e avremo:
![]()
L’equazione associata ammetterà come soluzione:
![]()
e quindi, andando a vedere la tabella delle disequazioni, il risultato sarà:
![]() .
.
Affinchè le due radici siano negative deve accadere che:
Andando a risolvere queste due disequazioni simultaneamente otterremo:
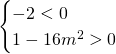
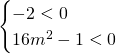
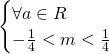
Intersecando le soluzioni, visto che queste comunque devono essere verificate contemporaneamente, si verifica subito che la soluzione richiesta è:
![]() .
.
Altri esercizi simili
- Esercizio 1 Equazioni parametriche
- Esercizio 2 Equazioni parametriche
- Esercizio 3 Equazioni parametriche
- Esercizio 4 Equazioni parametriche
- Esercizio 5 Equazioni parametriche
- Esercizio 6 Equazioni parametriche
- Esercizio 7 Equazioni parametriche
- Esercizio 8 Equazioni parametriche
- Esercizio 9 Equazioni parametriche
- Esercizio 10 Equazioni parametriche
- Esercizio 11 Equazioni parametriche
- Esercizio 12 Equazioni parametriche
- Esercizio 13 Equazioni parametriche
- Esercizio 14 Equazioni parametriche
- Esercizio 15 Equazioni parametriche
- Esercizio 16 Equazioni parametriche
- Esercizio 17 Equazioni parametriche
(Questa pagina è stata visualizzata da 593 persone)