Teoria sulla regola di Ruffini
Esempio 1
- Sia
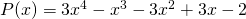
e
![]() ;
;
nella prima riga, andremo ad inserire i coefficienti della ![]() in ordine decrescente rispetto all’incognita. In basso a sinistra scriveremo il termine noto, invertendolo di segno.
in ordine decrescente rispetto all’incognita. In basso a sinistra scriveremo il termine noto, invertendolo di segno.
Riscriviamo ora il primo coefficiente di ![]() nell’ultima riga:
nell’ultima riga:
Moltiplichiamo adesso il valore appena scritto per il numero più a sinistra e lo inseriamo nella seconda riga; eseguiamo la somma in “verticale”:
Adesso ripetiamo lo stesso procedimento per gli altri coefficienti, moltiplichiamo per il numero a sinistra e sommiamo…
Il fatto che l’ultimo numero sia ![]() implica che la divisione è senza resto, e i numeri nell’ultima riga rappresentano i coefficienti dell’incognita del polinomio di grado abbassato di
implica che la divisione è senza resto, e i numeri nell’ultima riga rappresentano i coefficienti dell’incognita del polinomio di grado abbassato di ![]() rispetto a
rispetto a ![]() .
.
Quindi:
![]()
![]()
Potrebbe interessarti anche:
(Questa pagina è stata visualizzata da 2127 persone)